结构分析有限元程序应用：分析单元的建立和表达式推导

有了推导出的位移函数和形函数，就可以进一步导出单元的几何矩阵、应力矩阵和单元刚度矩阵以及外力等效节点力。单元的分析是为了建立单元的刚度矩阵，建立刚度矩阵的方法有直接刚度法、虚功原理法、能量变分法、加权参数法。其中，直接刚度法是直接应用物理概念来建立单元的有限元方程和分析单元特性的一种方法。这一方法仅适用于简单形状的单元，例如梁单元。下面利用变分原理中的虚位移原理来建立单元的刚度矩阵。

前面已经推导了用3个节点的坐标和位移表示单元内各点的位移：

对单元来说，节点力是通过节点作用于单元的外力。假设单元各节点有虚位移，那么单元内存在虚应变。设作用在单元节点上的力为iF、jF、mF，则单元节点力列阵为：

节点力在节点虚位移上做的虚功等于单元内部应力在虚应变上做的虚功。单元在节点处发生虚位移，产生相应的虚应变：

节点力在虚位移上所做的虚功为：

单元内储能的应变能为：

式中　t为厚度。

且节点位移仅与节点坐标有关，因此

其中

根据虚位移原理可知外力虚功等于内力虚功：

消去，则有(www.xing528.com)

由于三角形单元为常应变-常应力单元，且厚度t也为常数，设单元面积为A，则式（2-11）可写作：

简写为

式中就是要求的单元刚度矩阵。式（2-13）为表示单元节点力与节点位移关系的单元特性方程。

将平面应力问题中的弹性矩阵[D]、应变矩阵[B]的表达式代入式（2-14）中，可得单元刚度矩阵的分块表达式为：

其中　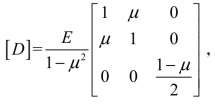称为平面应力问题的弹性矩阵；

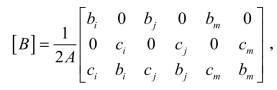称为应变矩阵。

将式（2-15）代入式（2-13）并展开得：

从式（2-16）可以看出，单元刚度矩阵每个分块阵的物理意义为：当在一个节点处产生单位位移而其他节点位移为零时，在该节点上需要的力的大小。例如ijk表示在j节点产生单位位移、其他节点位移为零时，需要在i节点上施加的力。

为奇异阵的物理意义：在无约束的条件下，单元可以作刚体运动。