【摘要】：项数由单元自由度决定，以3节点三角形单元为例，它有6个自由度，可以确定6个待定系数，因此这种三角形单元位移函数为：式（2-2）为线性多项式，称为线性位移函数，相应的单元称为线性单元。式（2-7）、（2-8）就是单元位移的插值表达式，它表明只要知道了节点位移，就可通过形函数插值求出单元内任意一点的位移。换言之，节点位移通过形函数控制了整个单元的位移分布。
多项式的项数越多，逼近精度越高。项数由单元自由度决定，以3节点三角形单元为例，它有6个自由度，可以确定6个待定系数，因此这种三角形单元位移函数为：
式（2-2）为线性多项式，称为线性位移函数，相应的单元称为线性单元。
由于节点i、j、m在单元上，它们的位移自然也就满足位移函数（2-2）。设3个节点的位移值分别为
如图2-5。
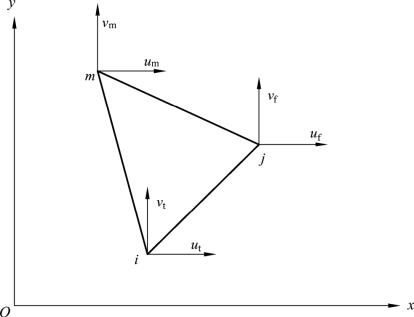
图2-5 三角形三节点单元
将节点位移和节点坐标代入式（2-2）得（以第一个方程为例）：
式（2-3）中共有3个方程，可以求出3个待定系数：
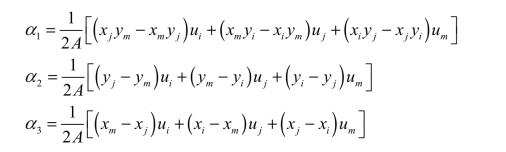
式中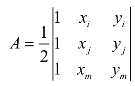 
为三角形单元的面积。
以上各式中的括号内都为已知的节点坐标值。令：
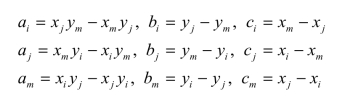
那么α1∼α3的值简写为：(www.xing528.com)
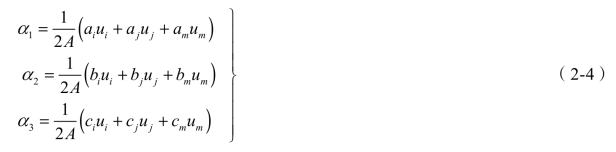
将式（2-4）代入式（2-2），便可得到用节点坐标和节点位移表示的位移函数式：
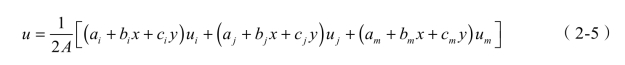
为书写方便，引入表达式：
式中 Ni、Nj、Nm称为形函数，它们是坐标的函数，与节点坐标有关，与节点位移无关。因此，式u、v表达式可以写为：
以矩阵表示为：
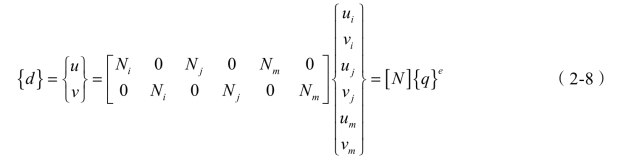
式中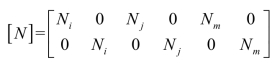 
称为形函数矩阵；
为单元节点位移矩阵。
式（2-7）、（2-8）就是单元位移的插值表达式，它表明只要知道了节点位移，就可通过形函数插值求出单元内任意一点的位移。换言之，节点位移通过形函数控制了整个单元的位移分布。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
