高等数学：函数平均值计算

在实际问题中，常常需要计算某一组数的平均值.例如用游标尺测量小球的直径n次，测得的数值为y1，y2，y3，…，yn，通常用它们的平均值

来作为这个球直径的大小.

在科学技术中，不仅要计算n个数的平均值，而且还常常要计算在某一区间上连续变化的函数的平均值.例如求平均电流、平均功率、平均电压等.

下面就来讨论连续函数f（x）在区间［a，b］上的平均值的定义及求法.先把区间［a，b］用分点

a=x0 ＜x1 ＜x2 ＜… ＜xn-1 ＜xn =b

分成n个相等的小区间，于是每个小区间的长度为这些分点处f（x）的函数值依次为f（x1），f（x2），…，f（xn）.

它们的算术平均值为

从公式（6.20）直观看出，可以用f（x1），f（x2），…，f（xn）的平均值来近似地表达函数f（x）在区间［a，b］上所有函数值的平均值，且n越大其近似程度越高.因此，令n→∞，把上述平均值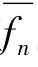的极限称为函数f（x）在区间［a，b］上的平均值，记为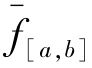，即

所以

上式表明，连续函数f（x）在区间［a，b］上的平均值等于它在区间［a，b］上的定积分除以区间［a，b］的长度.(www.xing528.com)

例6.25 一物体以速度v=3t2+2t（m/s）做直线运动，试计算它在t=0到t=3秒时段内的平均速度.

解 由式（6.21），物体的平均速度为

例6.26 设纯电阻电路中的正弦交流电流i=i（t）=Imsinωt，其中Im 为电流的最大值（即峰值），ω为角频率.求：

（1）在正半周期上的电流平均值（简称“平均电流”）；

（2）在一个周期上功率的平均值（简称“平均功率”）.

解 （1）由电工学知，正弦交流电的周期为则正的半周期为由式（6.21）得电流在上的平均值为

（2）设电阻为R（常数），于是电路中的电压为u=iR=ImRsinωt，从而功率为

所以，功率在一个周期的区间上的平均值为