【摘要】：根据万有引力定律，质量为m1和m2，相距为r的两质点之间的引力为其中K为引力常数，引力方向是沿着两质点的连线的方向.下面计算一根细棒对一个质点的引力.图6.29例6.22 设有一根长度为l、线密度为ρ的均匀细直棒，在其中垂线上距棒a单位处有一质量为m的质点A，试计算该棒对质点A的引力，如图6.29所示.解 取坐标系如图6.28所示，棒位于x轴上，中点为原点，质点A在y轴上，取x为积分变量，变化区间
根据万有引力定律，质量为m1和m2，相距为r的两质点之间的引力为
其中K为引力常数，引力方向是沿着两质点的连线的方向.
下面计算一根细棒对一个质点的引力.
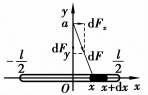
图6.29
例6.22 设有一根长度为l、线密度为ρ的均匀细直棒，在其中垂线上距棒a单位处有一质量为m的质点A，试计算该棒对质点A的引力，如图6.29所示.
解 取坐标系如图6.28所示，棒位于x轴上，中点为原点，质点A在y轴上，取x为积分变量，变化区间为
由于细棒上各点与质点A的距离不同，且各点对质点A的引力方向也不同，因此，不能直接应用式（6.19）来计算.
设想把细棒分成许多小段.在区间
上任取一小区间［x，x+dx］，把相应于［x，x+dx］的一段细棒近似看成位于x处的质点，其质量为ρdx，它与质点A的距离为r=
因此，由万有引力定律知，这段细直棒对质点A的引力ΔF的大小近似为(www.xing528.com)
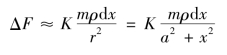
从而得到ΔF在铅直方向的分力ΔFy的近似值为
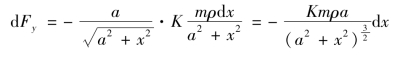
dFy是细棒对质点A的引力在铅直方向的分力Fy的元素，其中负号表示铅直分力的方向是朝下的（即与y轴的正向相反）.以dFy为被积表达式，取区间
上的定积分，便得引力在铅直方向的分力为
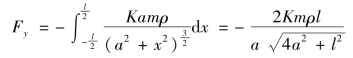
由于细棒关于y轴对称，因此引力在水平方向的分力Fx=0.所以细棒对质点A的引力大小为
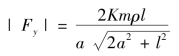
方向沿细棒的中垂线指向细棒.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
