液体压力与深度变化规律简介

由物理学知道，物体在液面下越深受到液体的压力就越大，通常用单位面积上所受的压力的大小——压强来衡量.压强p随液体深度的不同而变化，在夜面下深度为h处的压强为

p=γh

其中，γ=ρg为液体的容重，ρ为液体的密度，g为重力加速度.

如果有一面积为A的薄板水平地放置在液面下深度h处，那么薄板一侧所受的液体压力为

设有一薄板，形状如图6.26所示，垂直放在液体中.选取坐标系的x轴向下，y轴与液面相平，薄板的曲边方程为y=f（x），f（x）为连续函数，求液体对薄板一侧的压力P.

由于深度不同时压强不同，深度相同时压强相同.因此，可以设想把薄板分成许多水平的小横条.取x为积分变量，变化区间为［a，b］.在区间［a，b］上任取一小区间［x，x+dx］，现考虑相应于这个小区间上的小横条薄板，它可近似地看成水平放置在液面下深度为x的位置上，小横条的面积近似于小矩形的面积f（x）dx.于是，根据公式（6.17），小横条一侧所受压力ΔP的近似值，即压力元素为

dP=γxf（x）dx

图6.26

以γxf（x）dx为被积表达式，在区间［a，b］上作定积分，便得液体对薄板一侧的压力为

例6.20 一底为8cm、高为6cm的等腰三角形片，垂直沉没在水中，顶在上、底在下且与水面平行，而顶离水面3cm.试求它每面所受的压力P.

解 取坐标系如图6.27所示，x轴向下表示水深，y轴与水平面相平.取x为积分变量，其变化区间为［3，9］.

方程为

由于三角形片关于y轴对称，x轴两侧所受压力相等.由公式（6.18）得所求压力为(www.xing528.com)

其中水的容重γ=9.8×10-3N/cm3.

例6.21 一椭圆形闸门，长轴为2m、短轴为1.5m，短轴与水平面垂直，闸门顶与水面相齐，试求闸门所受的压力.

解 选取坐标如图6.28所示，取x为积分变量，变化区间为［-0.75，0.75］.右半椭圆的方程为

图6.27

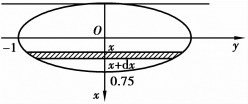
图6.28

由于闸门是关于x轴对称，两侧压力相等，闸门所受的压力等于右半闸门所受的压力的2倍.

在水深h=x+0.75处高为dx的右半横条所受压力近似于

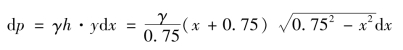
于是

其中水的容重γ=9.8kN/m3.