变力直线运动功，高数

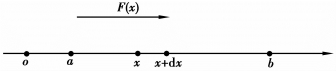
图6.21

设物体在变力F=F（x）的作用下沿直线（x轴）从点x=a移动到点x=b，并设力的作用方向与物体的运动方向一致.F（x）在区间［a，b］上连续.求力F所作的功W，如图6.21所示.

如果力F是常量，那么力F对物体所作的功为W=F·（b-a），但此问题中力F=F（x）不是常量，而是x的函数，因此，不能按常力情形的公式来计算.下面用元素法来求功W.

取x为积分变量，变化区间为［a，b］，在区间［a，b］上任取一个小区间［x，x+dx］，由于F（x）在区间［a，b］连续，因而力在这个小区间上的变化很小，所以相应于小区间［x，x+dx］上变力所作的功ΔW近似于在点x处的力F（x）与小区间［x，x+dx］的长度dx的乘积，即

ΔW≈F（x）dx

记dW=F（x）dx，称为功元素.于是

由式（6.16）知，求变力作功时只要能正确地找到变力函数，再求定积分即可.

例6.16 在底面积为S的圆柱形容器中盛有一定量的气体，在等温条件下，由于气体的膨胀，把容器中的一个活塞（面积为S）从a点处推移到b点处（图6.22），计算活塞移动过程中气体压力所作的功W.

解 取坐标如图6.22所示，活塞的位置可用坐标x来表示.由公式（6.16）知，只要写出区间［a，b］上任一点x处的气体压力F（x）.据物理学知，一定量的气体在等温条件下，压强P与体积V的乘积为常数K，即

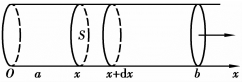
图6.22

因为V=xS，所以从而得到作用在活塞上的力

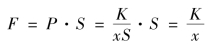
根据公式（6.16），便得所求功为

例6.17 自地面垂直向上发射火箭，火箭质量为m.试计算将火箭发射到距离地面的高度为h处所做的功，并计算第二宇宙速度（即火箭脱离地球引力范围所具有的速度）.

解 取坐标系如图6.23所示，r轴垂直向上，原点在地球的中心.设地球质量为M，半径为R.为了发射火箭，必须克服地球引力，由万有引力定律知，地球对距地心r（≥R）处的火箭的引力为

其中，r为火箭到地球中心的距离，K为引力常数.

由于火箭在地面（r=R）时，地球对火箭的引力为mg（g为重力加速度），即

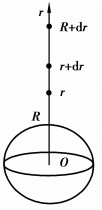
图6.23

从而

于是，引力为

根据公式（6.16），将火箭自地面（r=R）发射到距离地面高度为h（r=R+h）时，克服地球引力所作的功为(www.xing528.com)

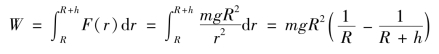
使火箭脱离地球引力范围，可理解为使火箭无限远离地球，这时所做的功为

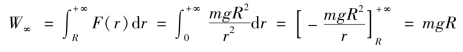
根据机械能守恒定律知，要使火箭能脱离地球引力范围，所需做的功W∞应等于火箭的初始动能是火箭离开地面的初始速度），即，故

将g=9.8（m/s2），R=6371（km）=6.371×106（m）代入上式右端，得

这个速度称为第二宇宙速度.

下面举几个克服重力作功的例子.

例6.18 一直径为20m的半球形水池，池内装满水，问要把池中的水抽尽需做多少功？

解 要将水池中的水抽出，池中的水升高到池口平面即可.因此，取坐标如图6.24所示，球心为原点，x轴向下表示水的深度，过球心的水平线为y轴，对这个坐标系来讲，图中半圆的方程为x2+y2=102.取x为积分变量，变化区间为［0，10］，由于不同深度的质点被提出时所上升的高度不同.所以，设想把池内水分成许多水平的薄层，于是在区间［0，10］上任取一小区间［x，x+dx］，考虑相应于这个小区间上的薄层水，深度为x处的水面面积为S（x）=πy2 =π（100-x2），此薄层水的体积近似于

图6.24

S（x）dx=π（100-x2）dx

并且把此薄层水的深度近似看成为x.这样，抽出此薄层水克服重力所做的功近似为

这就是功元素，其γ=ρg为水的容重，ρ为水的密度，g为重力加速度，γ=9.8kN/m3.于是，所求功为

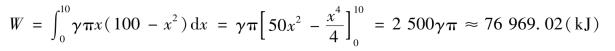
例6.19 一条长28m，质量为20kg的均匀链条被悬挂于某建筑物的顶部.问需做多大的功才能把这一链条全部拉上顶部？

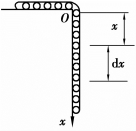
图6.25

解 取坐标系如图6.25所示，坐标原点在建筑物顶部，x轴向下表示链条的长度.质量为20kg的链条所受重力为

每米链条所受重力为

取x为积分变量，变化区间为［0，28］，在区间［0，28］上任取一小区间［x，x+dx］，链条上相应于这个小区间的重量为7dx，把这一小段距顶部的距离近似看成为x，则将此小段链条拉上建筑物顶部克服自身重力所做的功近似于

dw=7xdx

这就是功元素.于是所求功为