(1)弧长的概念
在初等几何中,圆周的长度是用圆内接正多边形的周长来逼近的,当正多边形的边数无限增加时的极限就等于圆周长.现在,我们用类似的方法来建立平面曲线的弧长的概念.设有一条以A、B为端点的弧(图6.17),在弧AB上任取分点:
A=M0,M1,M2,……,Mn-1,Mn =B
将弧AB分成n段,依次连接相邻分点得一条内接折线,如图6.18所示.
设每条弦的长度为![]() 则折线长度为
则折线长度为
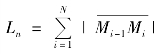
记![]() 如果当分点数目无限增加,且λ→0时,折线长度Ln的极限存在,则称此极限值为弧AB的弧长.这时,称这段弧AB是可求长的.
如果当分点数目无限增加,且λ→0时,折线长度Ln的极限存在,则称此极限值为弧AB的弧长.这时,称这段弧AB是可求长的.
(2)弧长的计算公式
1)直角坐标情形
问题:设弧AB由直角坐标方程
y=f(x) (a≤x≤b)
给出,其中f(x)在区间[a,b]上具有一阶连续导数,即弧AB是光滑曲线,求弧AB的长度S(图6.19).取横坐标x为积分变量,变化区间为[a,b],在区间[a,b]上任取一小区间[x,x+dx],曲线上相应于这个小区间上的一段弧的长度ΔS近似于曲线在点(x,f(x))处的切线上相应的一小段的长度,即
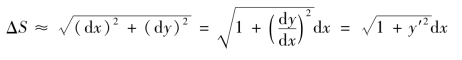
记![]() 称为弧长元素.
称为弧长元素.
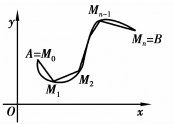
图6.18
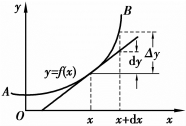
图6.19
以![]() 为被积表达式,在区间[a,b]上作定积分,便得所求弧长为
为被积表达式,在区间[a,b]上作定积分,便得所求弧长为
![]()
若弧AB的方程为
![]()
其中φ(y)在区间[c,d]上有一阶连续导数.类似可得弧AB的长度为
![]()
2)参数方程情形
若弧AB由参数方程 给出,其中φ(t),ψ(t)在区间[α,β]上具有连续导数.这时,弧长元素为
给出,其中φ(t),ψ(t)在区间[α,β]上具有连续导数.这时,弧长元素为
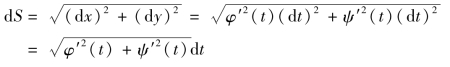
从而,所求弧的长度为
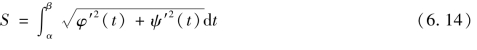
3)极坐标情形
若弧AB由极坐标方程
![]() (https://www.xing528.com)
(https://www.xing528.com)
给出,其中ρ(θ)在区间[α,β]上具有一阶连续导数.
由直角坐标与极坐标的关系可得以极角θ为参数的弧AB的参数方程为
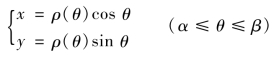
于是,弧长元素为
![]()
从而可得所求弧的长度为
![]()
例6.13 计算对数曲线y=lnx,从x=1到x=2之间一段弧的长度.
解 由于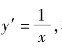 根据式(6.12),所求弧长为
根据式(6.12),所求弧长为
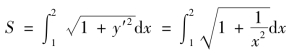
在以上积分中作代换![]() 则
则
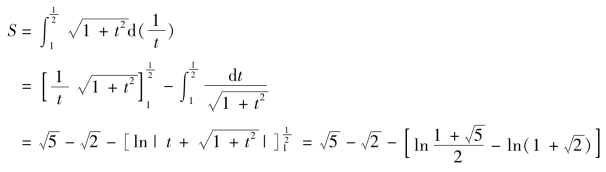
例6.14 计算星形线
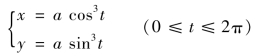
的全长,如图6.20所示.
解 由于对称性,星形线的全长是它在第一象限内弧长的4倍.在第一象限内![]() 由于
由于
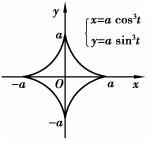
图6.20
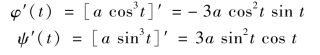
于是弧长元素为
![]()
所以,由式(6.4)得星形线的全长为
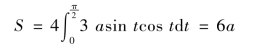
例6.15 求心形线ρ=a(1+cosθ)(a>0)的全长.
解 由对称性,心形线的周长为极轴上方部分弧长的2倍,由于
![]()
于是弧长元素为
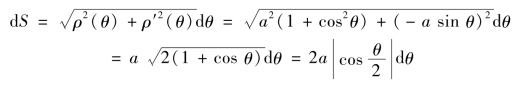
所以,由式(6.5)得心形线的周长为
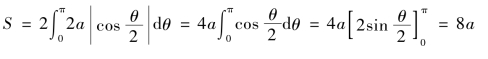
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




