体积-高等数学-特殊空间体积计算

这里只讨论两种比较特殊的空间体的体积.至于较一般的空间体体积的计算，将在下册中的重积分里讨论.

（1）平行截面面积为已知的空间体的体积

设有一空间体位于过点x=a、x=b且垂直于x轴的两个平面之间（如图6.12所示），过任一点x∈［a，b］作垂直于x轴的平面截得空间体的截面面积A（x）为已知的连续函数，求该空间体的体积V.

取x为积分变量，它的变化区间为［a，b］，在区间［a，b］上任取一小区间［x，x+dx］，相应于此小区间上的薄空间体的体积ΔV近似于底面面积为A（x）、高为dx的正柱体（上、下底的面积都是A（x）的体积，即ΔV≈A（x）dx，从而得到体积元素dV≈A（x）dx.

以A（x）dx为被积表达式，在区间［a，b］上作定积分，得所求空间体的体积为

例6.6 有一空间体，以长半轴a=10、短半轴b=5的椭圆为底，而垂直于长轴的截面都是等边三角形，求此空间体的体积.

解 取底面椭圆所在的平面为xOy平面，椭圆中心为原点，椭圆长轴在x轴上，椭圆短轴在y轴上，如图6.13所示.底面椭圆方程为，即.

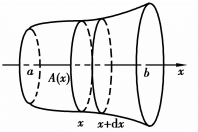
图6.12

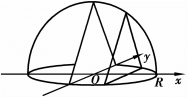
图6.13

取x为积分变量，变化区间为［-10，10］，在区间［-10，10］上任一点x处垂直于x轴的截面面积为

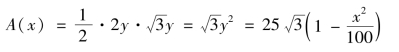
于是空间体的体积为

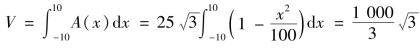
例6.7 两个底半径为R的圆柱体垂直相交，求它们公共部分的体积.

解 由于对称性，我们只画出图形的部分，并建立坐标系如图6.14所示.取x为积分变量，其变化区间为［0，R］，在区间［0，R］上任一点x处垂直于x轴的截面为一正方形，其边长为，其面积为A（x）=R2-x2.因此，由公式（6.8）得所求体积为

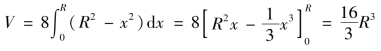
（2）旋转体的体积

旋转体就是平面图形绕平面上一条直线旋转一周而形成的空间体，这条直线称为旋转轴.圆柱、圆锥、圆台和球体等都可以看成旋转体.下面讨论旋转体体积的求法.

问题：设有一曲边梯形，它由连续曲线y=f（x）、直线x=a、x=b所围成.求此曲边梯形绕x轴旋转一周而形成的旋转体的体积V.

取x为积分变量，它的变化区间为［a，b］，在区间［a，b］上任取一小区间［x，x+dx］.相应于此小区间的窄曲边梯形绕x轴旋转而成的薄旋转体的体积ΔV近似于以f（x）为底半径、高为dx的扁圆柱体的体积（图6.15），即

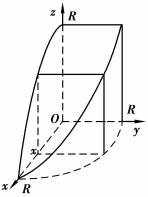
图6.14

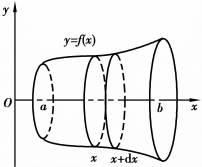
图6.15

从而得体积元素dV=π［f（x）］2dx，以π［f（x）］2dx为被积表达式在区间［a，b］积分，便得所求旋转体的体积

同理可得，由连续曲线x=φ（y）、直线y=c、y=d（c＜d）及y轴所围成的曲边梯形绕y轴旋转一周而成的旋转体的体积为

例6.8 计算由椭圆所围成的图形绕x轴旋转一周而成的旋转体的体积V.

解 这个旋转体可看成是由上半椭圆

与x轴围成的图形绕x轴旋转而成的旋转体.利用公式（6.9），得

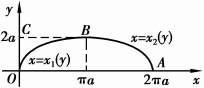
图6.16

例6.9 计算由摆线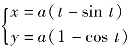的第一拱（0≤t≤2π）与x轴所围成的图形，如图6.16所示.分别绕x轴、y轴及直线y=2a旋转而成的旋转体的体积.(www.xing528.com)

解 （1）绕x轴旋转根据公式（6.9），所述图形绕x轴旋转而成的旋转体的体积为

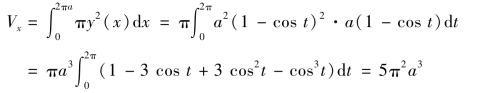
（2）绕y轴旋转

把摆线的第一拱分为两段弧OB（0≤t≤π）与BA（π≤t≤2π），OB和BA的方程分别用x=x1（y）、x=x2（y）表示.所述图形绕y轴旋转而成的旋转体的体积可看成平面图形OABC与OBC（图6.16）分别绕y轴旋转而成的旋转体的体积之差.因此，根据公式（6.10）所求体积为

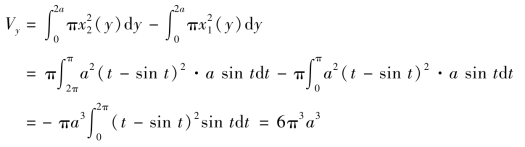
（3）绕y=2a旋转

取x为积分变量，变化区间为［0，2πa］，在区间［0，2πa］上任取一点x，该点垂直于x轴的截面为一个以（2a-y）为内圆半径、以2a为外圆半径的圆环，其面积为

π（2a）2-π（2a-y）2 =πy（4a-y）

因此，所求体积为

上面计算旋转体的体积时，所取的体积元素是垂直于旋转轴的扁柱体.当采用这种方法在计算某些旋转体的体积时会很不方便，所以，有时也可采用另外的方法，请看下面两个例子.

例6.10 求由连续曲线y=f（x）（f（x）≥0）、直线x=a、x=b（b＞a＞0）及y=0所围成曲边梯形绕y轴旋转而成的旋转体的体积.

解 取横坐标x为积分变量，变化区间为［a，b］，在区间［a，b］上任取一小区间［x，x+dx］，相应于该小区间上的小曲边梯形绕y轴旋转而成的旋转体的体积ΔV近似于以dx为底、高为f（x）的小矩形绕y轴旋转而成的旋转体的体积，也就是ΔV近似于以x和x+dx分别为底半径而高为f（x）的两圆柱体体积之差，即

ΔV≈π（x+dx）2f（x）-πx2f（x）=π·2xf（x）dx+πf（x）（dx）2

上式中，因f（x）有界，故πf（x）（dx）2是比dx更高阶的无穷小.所以，取体积元素为

dV=2πxf（x）dx

以体积元素作为被积表达式在区间［a，b］作定积分，得所求旋转体的体积

例6.11 求由曲线y=2x-x2与x轴所围的图形绕y轴旋转而成的旋转体的体积.

解 先求出曲线y=2x-x2与x轴的两个交点在位于x=0及x=2处.

取横坐标x为积分变量，其变化区间为［0，2］，由公式（6.11）得所求旋转体的体积为

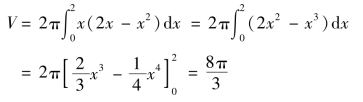
读者不妨用这种方法再计算一下例6.9的第二部分（绕y轴旋转部分），并与那里的计算过程作比较.

例6.12 一个瓷质坩埚，外高H=10cm，比重2.5g/cm3，坩埚的内壁与外壁是由抛物线旋转而成的，把它铅直地浮于水盆内，如果坩埚盛有高为h=2cm的水银（比重13.5g/cm2），问坩埚浸入水中有多深（图6.17）.

解 先求出坩埚质量.

其体积为：

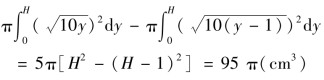
于是坩埚质量为：95π×2.5=237.5π（g）

再求出水银质量：

水银的体积为：

水银的质量为：5π×13.5=67.5π（g）

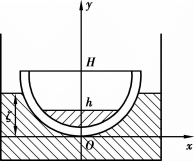
图6.17

设坩埚浸入水中的深度为ζ（cm）.

由阿基米德原理：

排开水的体积：

故排开水的质量：5πζ2×1=237.5π+67.5π

因此