【摘要】:如果函数f(x)在点x0的任一邻域内都无界,则称点x0为f(x)的瑕点,无界函数的广义积分也称为瑕积分.否则就称广义积分发散.注意:广义积分的记号与定积分相同,但含义却不一样.例5.41 计算广义积分.解 因为所以点a是被积函数的瑕点,于是有为了方便起见,也可仿照牛顿-莱布尼茨公式的形式,设F(x)是被积函数f(x)在积分区间上的一个原函数,若记则式(5.25)、式(5.26)便可记为;而式(5.
如果函数f(x)在点x0的任一邻域内都无界,则称点x0为f(x)的瑕点,无界函数的广义积分也称为瑕积分.
否则就称广义积分![]() 发散.
发散.
注意:广义积分的记号![]() 与定积分相同,但含义却不一样.
与定积分相同,但含义却不一样.
例5.41 计算广义积分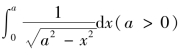 .
.
解 因为
所以点a是被积函数的瑕点,于是有
为了方便起见,也可仿照牛顿-莱布尼茨公式的形式,设F(x)是被积函数f(x)在积分区间上的一个原函数,若记
则式(5.25)、式(5.26)便可记为![]() ;而式(5.27)便可记为
;而式(5.27)便可记为![]()
![]()
例5.42 计算下列广义积分:
解 (1)因为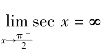 ,故点
,故点![]() 为被积函数的瑕点.
为被积函数的瑕点.
由于
所以,此广义积分发散.
(2)因为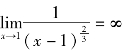 ,所以点1为被积函数的瑕点.于是
,所以点1为被积函数的瑕点.于是
(3)因为![]() ,点0为被积函数的瑕点,于是
,点0为被积函数的瑕点,于是
例5.43 证明广义积分![]() 当q<1时收敛,当q≥1时发散,其中a<b.
当q<1时收敛,当q≥1时发散,其中a<b.
证明 当q=1时,
当q≠1时,(https://www.xing528.com)
因此,当q<1时,广义积分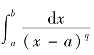 收敛,其值为
收敛,其值为 当q≥1时发散.
当q≥1时发散.
特别地,当a=0,b=1时,上述积分变为![]() 于是可知广义积分
于是可知广义积分![]() 当q<1时收敛,其值为
当q<1时收敛,其值为![]() 当q≥1时发散.
当q≥1时发散.
例5.44 讨论广义积分![]() 的敛散性.
的敛散性.
解 因为![]() ,所以x=0是被积函数的瑕点,于是
,所以x=0是被积函数的瑕点,于是
由例5.43知,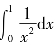 发散,故
发散,故![]() 发散.
发散.
如果疏忽了x=0是被积函数的瑕点,而按定积分计算,便得到以下错误的结果:
例5.45 计算广义积分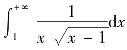 .
.
解 因为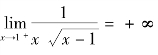 ,这既是无穷区间上的广义积分,又是无界函数的广义积分.
,这既是无穷区间上的广义积分,又是无界函数的广义积分.
设![]() =t,即x=t2+1,dx=2tdt.当x=1时,t=0;当x→+∞时,t→+∞.于是
=t,即x=t2+1,dx=2tdt.当x=1时,t=0;当x→+∞时,t→+∞.于是
注意:定积分的换元积分法与分部积分法一般都可以用到广义积分中来.
例5.46 计算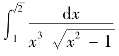 .
.
解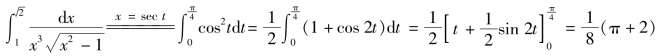
例5.47 计算![]()
解 由于被积函数以π为周期且连续,于是有
注意下述解法是错误的:
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




