高等数：无穷区间的广义积分

考虑介于曲线之下，x轴之上和直线x=1右侧的无穷区域的面积S，如图5.8（a）阴影部分所示.由于是无穷区域，所以往往认为它的面积也是无穷大，为了说明这个问题，下面仔细地分析一下.

先考虑无穷区域从直线x=1到x=b的那一部分，如图5.8B.中阴影部分所示的面积.其面积为

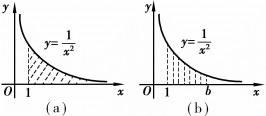
图5.8

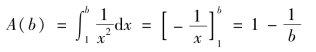
注意到不论b取多大，总有A（b）＜1成立.显然，b越大，A（b）越接近无穷区域的面积S，而且还发现

由于当b→+∞时，图5.8B.阴影部分的面积趋近于1，于是就认为无穷区域的面积S等于1，并且记作

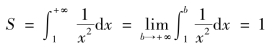
从这个例子得到启示：可以将函数在无穷区间上的积分定义为在有限区间上的积分的极限.

定义5.2 （1）设函数f（x）在区间［a，+∞）上连续，对任意的b＞a，如果极限存在，则称函数f（x）在无穷区间［a，+∞）上的广义积分收敛，并把此极限称为广义积分的值，即有

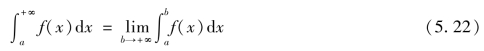
如果上述极限不存在，则称广义积分发散.

（2）设函数f（x）在区间（-∞，b］上连续，对任意的a＜b，如果极限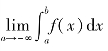存在，则称函数f（x）在无穷区间（-∞，b］上的广义积分收敛，并把此极限称为广义积分的值，即有

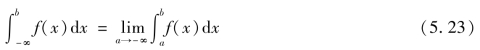(https://www.xing528.com)

如果上述极限不存在，则称广义积分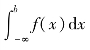发散.

（3）设函数f（x）在区间（-∞，+∞）上连续，c为任一实数.如果广义积分和都收敛，则称函数f（x）在无穷区间（-∞，+∞）上的广义积分收敛，且定义其值为

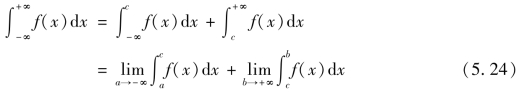
否则就称广义积分发散.

注：一般常取c=0.

有了广义积分的定义后，计算介于曲线之下，x轴之上和直线x=1右侧的无穷区域的面积S，就是计算一个广义积分

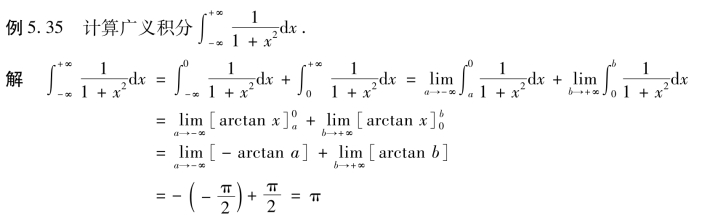
例5.35的描述太烦琐，为了方便，仿照牛顿-莱布尼茨公式的形式，设F（x）是被积函数f（x）在积分区间上的一个原函数.若记则式（5.22）、（5.23）、（5.24）分别可表示为

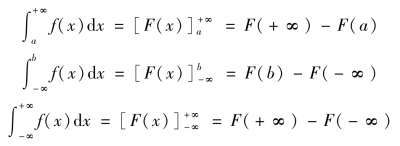
注：积分限+∞，-∞代入F（x）时，应理解为对F（x）求极限.

当p≠1时，