高等数学教材变限函数导数

设函数f（x）在闭区间［a，b］上连续，x为［a，b］上的任意一点，则f（x）在区间［a，x］上也连续，故f（x）在区间［a，x］上可积，即定积分存在.式中x既表示定积分的上限，又表示积分变量.

由于定积分与积分变量用什么符号无关，因此，为了不引起混淆，该定积分也常写成.当定积分上限x在［a，b］任取一值时，定积分就有一个确定的值与之对应，所以是上限x的函数，记为Φ（x），即

图5.7

这个函数Φ（x）称为变上限函数或变上限积分.

类似地，可定义变下限函数

由于所以，下面主要讨论变上限函数.

变上限函数Φ（x）具有下面的重要性质：

定理5.6（微积分基本定理） 如果函数f（x）在区间［a，b］上连续，则变上限函数在区间［a，b］上可导，且导数为

证明 任取x∈［a，b］，设x获得增量Δx（使x+Δx∈（a，b）），则函数Φ（x）相应的增量为

根据积分中值定理，得

ΔΦ（x）=f（ξ）Δx，ξ在x与x+Δx之间

上式两端同除以Δx，得

由于f（x）在［a，b］上连续，而当Δx→0时，有ξ→x.

所以

于是

(www.xing528.com)

即

Φ′（x）=f（x）

当x取a或b时，以上Δx→0分别改为Δx→0+或Δx→0-，可得

Φ′+（a）=f（a）与Φ′-（b）=f（b）

需要指出的是，变上限函数（5.14）是表示函数关系一种新的方法，用这种方法表示的函数在物理、化学、统计学中有着广泛的应用.例如，以法国著名物理学家菲涅耳（Fresnel，1788—1827）的名字命名的菲涅耳函数就是其中一例，这个函数最初出现在光波衍射的菲涅耳定理中，现在它已经被应用于高速公路的设计中.

定理5.6具有重要的理论意义与实用价值.它一方面揭示了微分与积分之间的联系，表明变上限函数对上限的导数等于被积函数在上限处的值.另一方面，它断言每个连续函数是另外一个函数的导数，由此得到原函数存在的一个充分条件.

定理5.7 若函数f（x）在区间［a，b］上连续，则f（x）在［a，b］上一定存在原函数，且变上限函数就是它的一个原函数.

由定理5.6，容易得到下面的推论：

推论5.3 设函数f（x）在区间［a，b］上连续，v（x）在［α，β］上可导，且当x∈［α，β］时，v（x）∈［a，b］，则

证明 将视为由与v（x）复合而成的复合函数.根据复合函数求导法

则，得

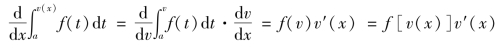
推论5.4 设函数f（x）在区间［a，b］上连续，u（x）、v（x）在［α，β］上可导，且当x∈［α，β］时，u（x）∈［a，b］、v（x）∈［a，b］，则

证明 任取c∈［a，b］，则

两边对x求导，由推论5.3即得所要证明的结论.

例5.5 求下列各函数的导数：