高等数-分部积分法解析

前面所介绍的换元积分法虽然可以解决许多积分的计算问题，但有些积分，如∫xsinxdx等，利用换元积分法无法求解.本节介绍另一种基本积分法——分部积分法.

由两个函数乘积的导数公式（uv）′=u′v+uv′移项，得

两边求不定积分，则有

公式（4.3）称为分部积分公式.还可简记为

定理4.4 设u=u（x），v=v（x）具有连续导数，则

根据式（4.3），求积分∫udv的问题化成了求积分∫vdu的问题.后一个问题可能比前一个问题简单，从而对计算有利.

例4.49 求∫x·cosxdx.

解 设u=x，dv=cosxdx，那么du=dx，v=sinx，代入分部积分公式（4.3），得

但若设u=cosx，dv=xdx，那么

于是

上式右端的积分比原积分更不容易求出.

由此可见，如果u和dv选取不当，就求不出结果，所以应用分部积分法时，恰当选取u和dv是一个关键，选取u和dv一般要考虑下面两点：

①v要容易求得；

②∫vdu要比∫udv容易积出.

例4.50 求∫x2·exdx.

解 设u=x2，dv=exdx，那么du=2xdx，v=ex.

于是

∫x2·exdx=x2·ex-2∫x·exdx

这里∫x·exdx比∫x2·exdx容易求积分，因为被积函数中x的幂次前者比后者降低了一次.对∫x·exdx再使用一次分部积分法：

设u=x，dv=exdx，那么du=dx，v=ex，从而

∫x·exdx=xex-∫exdx=xex-ex+C

于是

∫x2·exdx=x2·ex-2（xex-ex）+C=（x2-2x+2）ex+C.

一般地，对于积分∫xn·eaxdx，∫xn·sinbxdx，∫xn·cosbxdx等，用分部积分法求，并把xn取作u，余下部分取作dv.因这样用一次分部积分法就可以使幂函数的幂次降低一次，从而求原积分就化为求较简单的积分.

例4.51 求∫x2·lnxdx.

解 设u=lnx，dv=x2dx，那么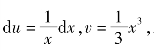利用分部积分法，得

例4.52 求∫x·arctanxdx.

解 设u=arctanx，dv=xdx，那么(www.xing528.com)

一般地，对于积分∫xn·lnxdx，∫xn·arctanxdx，∫xn·arcsinxdx，∫xn·arccosxdx等，分别把lnx，arctanx，arcsinx，arccosx等取作u，而把xndx取作dv.

例4.53 求∫ex·sinxdx.

解 ∫exsinxdx=∫sinxdex=exsinx-∫excosxdx

=exsinx-∫cosxdex

=exsinx-（excosx-∫exsinxdx）

所以

在积分的过程中往往要同时使用换元法与分部积分法.

例4.54 求

解 令则x=t2，dx=2tdt，于是

用分部积分法得

∫t·etdt=et（t-1）+C

于是

例4.55 求In=∫sinnxdx（n为正整数）.

解 当n=1，2时，积分为

现讨论n≥3的情形，利用分部积分公式，有

移项整理得

运用它可将被积函数的幂次降低，反复运用，最后得到积分∫sin2xdx或∫sinxdx，从而可以求出积分，例如n=4时，有

例4.56 求（a＞0，n为正整数）.

移项，整理得

若用n代替n+1，用n-1代替n，上式可改写成

如此下去，每用一次，n就降一次，最后出现的积分是n=1的情形.

此时，从而问题得到解决.

例4.57 已知f（x）有原函数ex2sinx，求∫xf′（x）dx.

解 由已知得f（x）=（ex2sinx）′=ex2（2xsinx+cosx），且∫f（x）dx=ex2sinx+C.

所以

例4.58 已知f′（ex）=1+x，求f（x）.

故