高等数学第二类换元法

第一类换元法是通过变量代换u=φ（x），引进新的积分变量u将积分∫f［φ（x）］φ′（x）dx化为积分∫f（u）du.下面将介绍的第二类换元积分法是选择适当的变量代换x=ψ（t）将积分∫f（x）dx化为积分∫f［ψ（t）］ψ′（t）dt，即有公式

当然，这个公式的成立是需要一定条件的，于是有第二类换元积分法.

定理4.3 设（1）x=ψ（t）是单调的、可导的函数，并且ψ′（t）≠0；

（2）f［ψ（t）］ψ′（t）具有原函数Φ（t），则Φ［ψ-1（x）］是f（x）的一个原函数（其中ψ-1（x）是x=ψ（t）的反函数），即有换元公式：

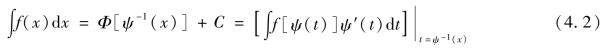
证明 令F（x）=Φ［ψ-1（x）］，利用复合函数的求导法则及反函数的导数公式，得

即F（x）是f（x）的原函数，于是有

解 和上例类似，可以利用1+tan2t=sec2t去掉根式.

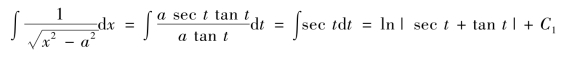
为了把sect及tant换成x的函数，我们根据作辅助三角形，如图4.4所示.

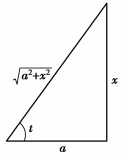
图4.3(www.xing528.com)

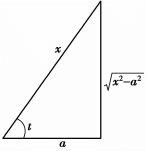
图4.4

于是有因此

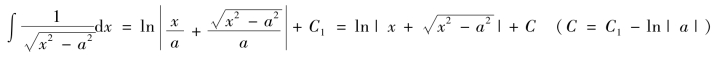
这三个例子所用的方法称为三角函数代换法，现将常用的几种代换归纳如下：

如被积函数中含有根式：

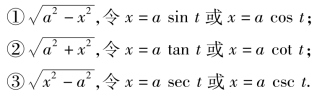
在具体解题时应根据被积函数的具体情况，选尽可能简捷的代换，不要拘泥于上述的变量代换.

下面介绍一种常用的代换——倒代换.

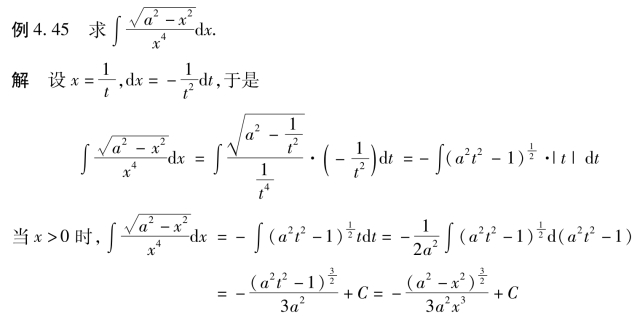
当x＜0时，有相同的结果.故无论何种情形，总有

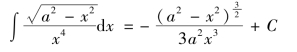
下面再给出几个常见的基本积分公式：