高等数学：曲率的概念及其计算

曲率是比较曲线弯曲程度大小的一个概念.

实际工作中，我们将会经常用到曲率的概念.如在结构力学当中，一个模件的强度大小，它不仅涉及构成模件的材料的种类，而且要涉及其形状弯曲程度问题.

如何比较曲线的弯曲程度呢？

假设两曲线段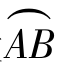和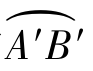′的长度一样，都是Δs，但它们切线的变化不同.对第一条曲线说来，在A点有一条切线 A，我们设想A点沿着曲线运动到B点，于是切线也跟着变动，变为在点B的切线 B，A与 B之间的夹角Δφ1就是从A到B切线方向变化的大小.同样，在第二条线上，Δφ2是从A′到B′切线方向变化的大小.在图上很容易看出Δφ1＜Δφ2，第二条曲线段比第一条曲线段弯曲得厉害些.由此可见，角度变化Δφ大，弯度也大.如图3.22至图3.24所示.

但是切线方向变化的角度Δφ还不能完全反映曲线的弯曲程度.如图3.25所示，两段长度分别为Δs，Δs′的圆弧切线方向改变了同一角度Δφ，但可明显看出弧长小的一段弯曲程度大.

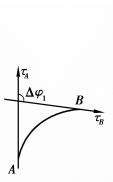
图3.22

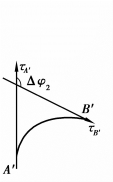
图3.23

图3.24

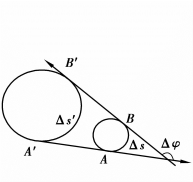
图3.25

从以上的分析，可见曲线的弯曲程度不仅与其切线方向变化的角度Δφ的大小有关，而且还与所考察的曲线段的弧长Δs有关，因此，一段曲线的弯曲程度可用

(www.xing528.com)

来衡量.其中Δφ表示曲线段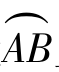上切线方向变化的角度，Δs为这一段曲线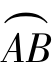的弧长，称其为曲线段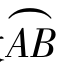的平均曲率，它刻画了这一段曲线的平均弯曲程度，如图3.26所示.

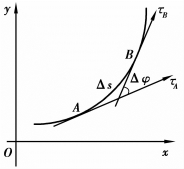
图3.26

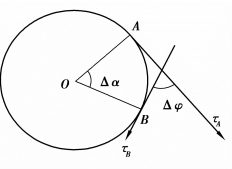
图3.27

如图3.27所示，对于半径为R的圆来说，圆周上任意弧段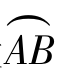的切线方向变化的角度Δφ等于半径OA和OB之间的夹角Δα.又弧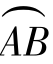的长度Δs=R·Δα，所以曲线段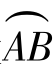的平均曲率为

上式说明圆周上的平均曲率为一个常数为半径的倒数.

对于直线来说，因沿着它切线方向没有变化，即这表示直线上任意一段的平均曲率都是零或者说“直线不曲”.

对于一般的曲线来说，如何刻画它在一点A处的弯曲程度呢？

从图3.26中可以看到：如果把Δs取得小一些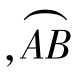弧段上的平均曲率也就能比较精确地反映出曲线在A点处的弯曲程度.随着B点越来越靠近A点，弧长Δs越来越小（当然Δφ也随之变化），也就越来越精确地刻画出在A点的弯曲程度.因此，我们就把极限

叫作曲线在A点的曲率.这个极限也就是导数，记为