【摘要】：定义3.3 若中至少有一个成立，则称直线y=C为曲线y=f（x）的水平渐近线.例3.39 求的渐近线.解所以y=0为其水平渐近线.定义3.4 若中至少有一个成立，则称直线x=x0为曲线y=f（x）的垂直渐近线.例3.40 求的渐近线.所以x=1为其垂直渐近线.定义3.5 设P为曲线y=f（x）上的动点，L为一条定直线，如果当P沿曲线无限远离原点时，点P与直线L的距离也随之趋于零，则称直线L为曲线y
定义3.3 若
中至少有一个成立，则称直线y=C为曲线y=f（x）的水平渐近线.
例3.39 求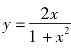
的渐近线.
解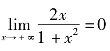
所以y=0为其水平渐近线.
定义3.4 若
中至少有一个成立，则称直线x=x0为曲线y=f（x）的垂直渐近线.
例3.40 求
的渐近线.
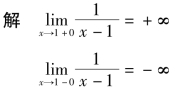
所以x=1为其垂直渐近线.
定义3.5 设P为曲线y=f（x）上的动点，L为一条定直线，如果当P沿曲线无限远离原点时，点P与直线L的距离也随之趋于零，则称直线L为曲线y=f（x）的斜渐近线，如图3.21所示.
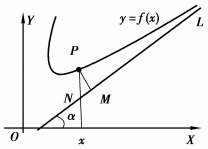
图3.21
设曲线y=f（x）有斜渐近线L（图3.21），其方程y=ax+b.于是曲线y=f（x）上任一点P（x，y）到L的距离PM=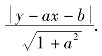
由于L是渐近线，所以
即
所以
得
(www.xing528.com)
如果曲线y=f（x）有斜渐近线L，则极限（2）存在，由此式求得a，再由式（1）可求得
反过来，如果式（2），（3）成立，则式（1）也成立，那么y=ax+b就是y=f（x）的渐近线.
综上所述，求斜渐近线的步骤如下：
①先求
（如果存在）；
②再求
（如果存在）；
③斜渐近线为y=ax+b.
例3.41 求y=x+arctanx的渐近线.
解
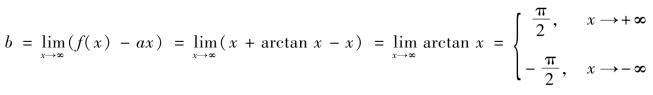
所以x→+∞时，有斜渐近线
时，有斜渐近线
例3.42 求函数
的渐近线.
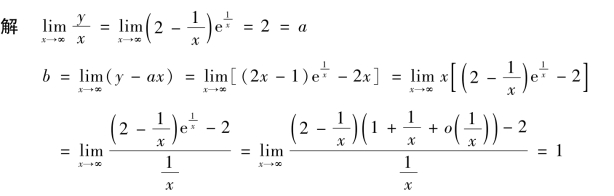
所以有斜渐近线y=2x+1
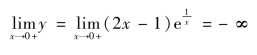
所以x=0为其垂直渐近线.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
