高等数学函数图形的凹凸性与拐点

图3.18

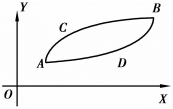
有了函数的单调性，有了函数的极值，就有了函数的大致轮廓.但函数单调的形态是有所不同的.如图3.18，弧ACB与弧ADB都是单调增加，它们就存在着区别，这就是函数的凹凸性.

仔细观察弧ACB与弧ADB，分析它们的异同.

对于弧ADB，在其上任取两点，过这两点作弦，在这两点之间的曲线段总是位于弦的下方.而对于弧ACB，在其上任取两点，过这两点作弦，在这两点之间的曲线段总是位于弦的上方.

若弧ADB、弧ACB是光滑的，也可用切线的方法来描述它.对于弧ADB，在其上任意一点作切线，切线总是位于曲线的下方.而对于弧ACB，在其上任意一点作切线，切线总是位于曲线的上方.

下面就用作弦的方法来定义凹凸性.

定义3.2 设f（x）在［a，b］上连续，如果对［a，b］内任意两点x1，x2，x1≠x2，恒有

那么称f（x）在［a，b］上的图形是（向上）凹的（或凹弧）.如果恒有

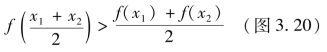
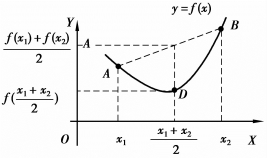
图3.19

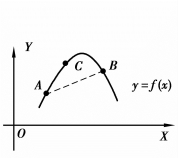
图3.20

那么称f（x）在［a，b］上的图形是（向上）凸的（或凸弧）.

例3.33 证明：f（x）=lnx的图形在（0，+∞）内是凸的.

证明 任取两点x1，x2∈（0，+∞），设x1＜x2，有

所以f（x）=lnx的图形在（0，+∞）内是凸的.

用定义判别函数图形的凹凸性往往比较困难，下面给出一个简便的判定法.

定理3.10 设f（x）在（a，b）内具有一阶和二阶导数，那么

（1）若在（a，b）内f″（x）＞0，则f（x）在（a，b）上的图形是凹的；

（2）若在（a，b）内f″（x）＜0，则f（x）在（a，b）上的图形是凸的.

证明 （1）设x1，x2为（a，b）内任意两点，且x1＜x2.

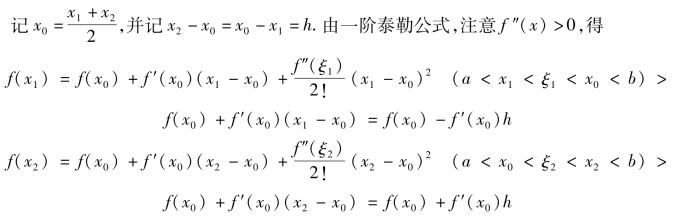
两式相加，得

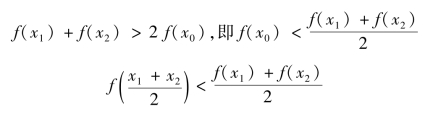
这说明f（x）在（a，b）上的图形是凹的.

同理可证（2）.

例3.34 判断函数y=2x3+3x2-12x+14的凹凸性.

解 函数的定义域为（-∞，+∞）(www.xing528.com)

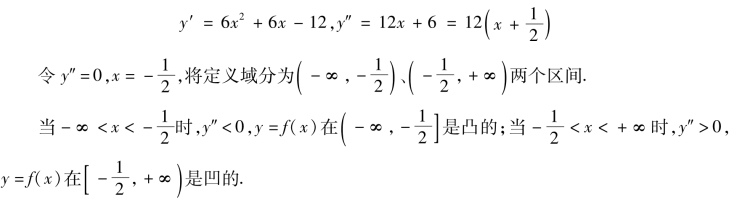
如果曲线y=f（x）在经过（x0，f（x0））时，曲线的凹凸性改变了，那么就称点（x0，f（x0））为这曲线的拐点.

如何寻找曲线y=f（x）的拐点呢？

我们知道，由f″（x）的符号可以判定曲线的凹凸性，如果f″（x0）=0，而f″（x）在x0的左右两侧邻近异号，那么点（x0，f（x0））就是一个拐点.值得注意的是f″（x）不存在的点也可能是f″（x）的符号发生变化的分界点，也可能有拐点.综上所述，求连续曲线y=f（x）的拐点可按如下步骤进行：

①求f″（x），并令f″（x）=0，求出根，再找出f″（x）不存在的点x1，x2，…，xn；

②x1，x2，…，xn把f（x）的定义域分为部分区间，讨论每个部分区间f″（x）的符号；

③列表讨论，找出凹凸区间及拐点.

例3.35 求函数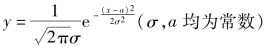的凹凸区间及拐点.

解 定义域为（-∞，+∞）

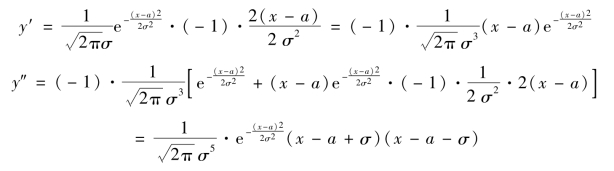
令y″=0，x=a-σ，a+σ，现列表讨论如下：

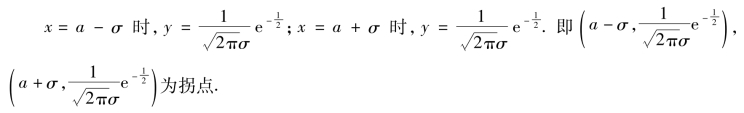
例3.36 求曲线y=e-x2的凹凸区间及拐点.

解 先求出函数的一、二阶导数：y′=-2xe-x2，y″=（4x2-2）e-x2.

令y″=0，解得现列表讨论如下：

例3.37 求曲线的拐点.

解 这函数在（-∞，+∞）内连续，当x≠0时

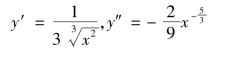
当x=0时，y′，y″都不存在，故二阶导数在（-∞，+∞）内不连续，且不具有零点，但x=0是y″不存在的点，它把（-∞，+∞）分成两个部分：（-∞，0），（0，+∞）.

在（-∞，0）内，y″＞0，函数图形在（-∞，0）内是凹的；

在（0，+∞）内，y″＜0，函数图形在（0，+∞）内是凸的.

故点（0，0）是这曲线的拐点.

例3.38 证明：xlnx+ylny＞（x+y）ln，（x＞0，y＞0，x≠y）.

证明 令f（x）=xlnx，x∈（0，+∞），则

所以f（x）在（0，+∞）为凹的，∀x，y∈（0，+∞）x≠y，有

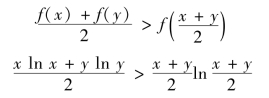
所以