高等数学上册：函数的最大值和最小值问题

在实际问题中，我们经常需要考虑如何花费最小代价去获取最大收益问题，如生产易拉罐时，要考虑在一定容积下，如何确定它的底面半径和高才能使得用料最省？又如一根圆木锯成矩形横梁时，怎样选择矩形的长和宽，才能使横梁的强度最大？这类“最大”“最小”“最省”的问题，在数学上可归结为求某一函数的最大值和最小值，简称为“最值问题”.

最值不同于前面讲到的极值.最值是一个整体概念，函数的最大值、最小值是在某个范围内考虑，而函数的极值是一个局部概念，只是在点的邻近考虑，这两个概念是不同的，因此函数的极大值或极小值不一定是它的最大值或最小值.

闭区间上的连续函数一定存在最大、最小值，最值有可能在区间内部取得，这时最值就是函数在区间上的极值.最值还有可能在端点处取得，所以闭区间上的连续函数的最值可用如下方法求得：

若函数f（x）在［a，b］上连续，求出函数f（x）在（a，b）内的所有驻点及不可导点，将函数f（x）在这些点的函数值与f（a）、f（b）相比较，其中最大的便是f（x）在［a，b］上的最大值，最小的便是f（x）在［a，b］上的最小值.

例3.26 求函数f（x）=x5-5x4+5x3+1在区间［-1，2］上的最大值与最小值.

解 f′（x）=5x4-20x3+15x2=5x2（x2-4x+3）=5x2（x-1）（x-3）

令f′（x）=0，得x=0，1，3，其中3∉［-1，2］.由

f（0）=1，f（1）=2，f（-1）=-10，f（2）=-7

所以f（x）在x=1处取得最大值2，在x=-1处取得最小值-10.

例3.27 求函数在［-3，4］上的最大值与最小值.

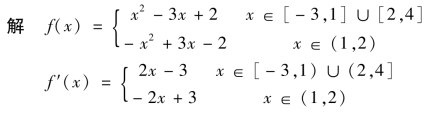
令f′（x）=0，得驻点为不可导点为x=1和x=2，又

所以最大值M=f（-3）=20，最小值m=f（1）=f（2）=0.

在一些特殊情况下，求最大值或最小值的方法可以得到简化：

①如果函数f（x）在区间［a，b］上单调，则最值在端点处取得：

②如果函数f（x）在区间［a，b］上连续，在区间［a，b］内部只有一个极值点，这个极值点是极大（小）值点时，它就是最大（小）值点.

在很多实际问题中，常遇到这样的简单情况，函数f（x）在闭区间［a，b］上或开区间（a，b）内是可微的，由问题的实际情况，可以断定函数f（x）在这区间内部某一点处取得最大值（或最小值）；且f（x）在这区间内部又只有一个驻点，在这种情况下，立即就能断定这个驻点一定是最大值点（或最小值点）（如图3.15和图3.16所示）.

图3.15

图3.16

例3.28 求数列的最大项.

解 令

令f′（x）=0得驻点x=e，当0＜x＜e时，f′（x）＞0；当e＜x＜+∞时，f′（x）＜0，故x=e是极大值点，而f（x）在定义域内只有一个极大值点，故为最大值点.又f（2）-f（3）＜0，所以数列最大项对应n=3.

图3.17(www.xing528.com)

例3.29 设有一块边长为a的正方形铁皮，从其各角截去同样的小正方形，做成一个无盖方匣.问截去多少方能使做成的匣子之容积最大？

解 如图3.17所示，用x表示截去的小正方形的边长，则得盒子容积为

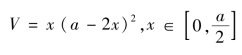
于是问题归结为求函数V=x（a-2x）2在上的最大值，因

V′=（a-2x）（a-6x）

令V′=0，在内有唯一解在端点时，V=0，故V必在时取得最大值.即当四角截去边长为的正方形时，所做成的盒子容积最大.

例3.30 某厂用铝合金生产装饮料用的易拉罐，为了安全，顶盖的厚度是罐身（侧面与底部）厚度的3倍（罐身整快材料，顶盖另装），问如何确定它的底面半径和高才能使用料最省？

解 设罐身的厚度为δ，则顶盖的厚度为3δ.记易拉罐的容积为V，底面半径为r，高为h=装饮料用的易拉罐容积恒定，所以V为常数.

罐身的用料（体积）为

而顶盖的用料为

U2（r）=3δπr2

因此问题归结为求函数

在（0，+∞）中的最小值.因此U′（r）在（0，+∞）只有唯一零点r0=而没有不可导点.又＞0，r∈（0，+∞），故r0是U（r）的最小值点.这时相应的高为即，当它的高为底面直径的2倍时用料最省.

最值问题也在社会科学尤其是经济科学中得到了广泛应用.因为经济活动的最重要目标之一就是用最小的花费去赢取最大的利润.

例3.31（销售总利润最大问题） 某工厂生产某种产品，年产量为x百台，总成本为C（x）万元，其中固定成本2万元，每生产100台，成本增加1万元，市场上每年可销售此种商品400台，其销售总收入为

问每年生产多少台，总利润为最大？在总利润最大的基础上再生产100台，总利润如何变化？

解 总成本C（x）=2+x，则

令L′（x）=0，得驻点x=3.因为L″（3）=-1＜0，所以x=3为极大值点，也是最大值点.因此每年生产300台，总利润为最大，最大利润为L（3）=2.5万元.又因为ΔL=L（4）-L（3）=-0.5万元，在总利润最大的基础上再生产100台，总利润将减少0.5万元.

利用函数的最大值和最小值还可以证明不等式.

例3.32 设p＞1，q＞1且，证明对任意x＞0，有

证明 设-x，x∈（0，+∞），f′（x）=xp-1-1.

令f′（x）=0得唯一驻点x=1，又知x=1为f（x）的极小值点，也是最小值点，且最小值故对任意x＞0，有f（1）=0，即