函数的极大极小值点及其性质

定义3.1 若f（x）在x0的邻域U（x0）内有定义，对∀x∈U° (x )0 都有f（x）＜f（x0）（或f（x）＞f（x0）），则称f（x）在x0取极大（小）值，x0称为极大（小）值点.极大值、极小值统称为极值，极大值点、极小值点统称为极值点.

函数的极值是一个局部概念，函数取得极值只是就其邻近区域的函数值进行比较.就整个考察区域而言，极小值有可能大于极大值.从几何直观上可以明显看到，如果把函数曲线的上下起伏看作大海里的波浪的话，极大值点、极小值点分别就是波峰、波谷，如图3.11所示.

那么，如何求函数的极值呢？进一步考察上面函数图像，可以看到，在函数取得极值处.如果此处存在切线的话，切线是水平的，如图3.11所示.当然，在图像中也可看到，具有水平切线的地方并不一定取得极值，如图3.12所示.此外，在图像中，在函数曲线不光滑的地方，也即是“尖点”处，函数有的取得极值（图3.13），有的不取得极值（图3.14）.

图3.11

图3.12

图3.13

图3.14

定理3.7（极值的必要条件） 若x0是f（x）的极值点，那么x0只可能是f′（x）的零点或者f（x）的不可导点.

x0是f（x）的极值点，若函数f（x）又在x0处可导，这事实上就是前面的费尔马定理.即可导函数的极值点必定是它的驻点，但反之不成立.例如函数f（x）=x3，它的导函数为f′（x）=3x2，有f′（0）=0，即x=0是这个可导函数的驻点，但x=0不是这函数的极值点，由函数单调性判别法则就知道该函数是严格单调增加的，它不可能有极值点，如图3.12所示.

此外，对于导数不存在的点，即“尖点”，函数也可能达到极值，例如由导数定义容易证明在x=0处f（x）左右导数存在，但不相等，即f′（0）不存在，但显然在x=0处有极小值f（0）=0，如图3.13所示.

综上所述，函数的极值点只可能在导数为零的点和不可导点处取得，至于这些点是不是极值点，还需进一步加以判断.

下面给出函数极值存在的充分条件.

定理3.8（极值存在的第一充分条件） 设函数f（x）在x0处连续，在x0的某去心邻域内可导.

①如果当x取x0左邻域的值时，f′（x）＞0；当x取x0右邻域的值时，f′（x）＜0，那么函数f（x）在x0处取得极大值；

②如果当x取x0左邻域的值时，f′（x）＜0；当x取x0右邻域的值时，f′（x）＞0，那么函数f（x）在x0处取得极小值.

证明 ①如果当x取x0左邻域的值时，f′（x）＞0，由f（x）在 [x，x0] 连续，在（x，x0）可导，根据拉格朗日中值定理，有

f（x0）-f（x）=f′（ξ）（x0-x） ξ∈（x，x0）

所以

f（x0）＞f（x）

当x取x0右邻域的值时，f′（x）＜0，类似可证有f（x0）＞f（x）.所以函数f（x）在x0处取得极大值.类似地可论证情形②.

也就是说：当x在x0邻近渐增地经过x0时，如果f′（x）的符号由正变负，那么f（x）在x0点处取得极大值；如果f′（x）的符号由负变正，那么f（x）在x0点处取得极小值.

例3.22 求函数的极值.

解 函数的定义域为（-∞，+∞）.

令f′（x）=0，得驻点另有不可导点x=1，它们将函数的定义域划分为列表讨论如下：

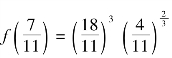可见为函数的极大值点，极大值为；x=1为函数的极小值点，极小值为f（1）=0；x=-1不是极值点.

例3.23 讨论函数的极值.(www.xing528.com)

解 函数的定义域为（-∞，-1）∪（-1，+∞）.

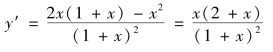
令y′=0，得驻点x=-2，x=0，它们将函数的定义域划分为（-∞，-2），（-2，-1），（-1，0），（0，+∞），列表讨论如下：

可见，x=-2为函数的极大值点，极大值为-4；x=0为函数的极小值点，极小值为0.

例3.24 求函数

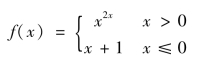
的极值.

解 因为

即f（x）在x=0处不可导，故

令f′（x）=0得驻点可能在及x=0有极值，列表讨论如下：

由表得知：x=0为f（x）的极大值点，极大值为f（x）的极小值点，极小值为.

极值存在的第一充分条件对于驻点和不可导点都是适用的，对于驻点情形，如果驻点处二阶导数不为零，还有进一步的判别方法.

定理3.9（极值存在的第二充分条件） 设f（x）在x0点处有二阶导数，且f′（x0）=0，f″（x0）≠0，那么：

①当f″（x0）＜0时，函数f（x）在x0处取得极大值；

②当f″（x0）＞0时，函数f（x）在x0处取得极小值.

证明 ①由于f″（x0）＜0，按照二阶导数的定义有

根据函数极限的保号性，存在，得

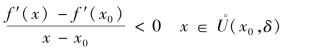
但f′（x0）=0，故上式为，列表讨论如下：

函数f（x）在x=x0处取得极大值，证毕.

类似地可证得情形②.

例3.25 求函数的极值.

解 先求出函数的一、二阶导数

令f′（x）=0，得函数的驻点x=-1，x=2，因为f″（-1）=-3e-1＜0，所以函数f（x）在点x=-1处达到极大值所以函数f（x）在点x=2处达到极小值.

注意，当驻点处有f″（x0）=0，定理3.9就不能应用.事实上，此时会有一个更一般的结论，见习题中第6题.当然，也可用极值存在的第一充分条件进行讨论.