高等数学：拉格朗日中值定理

（1）罗尔（Rolle）定理

定理3.2 若函数f（x）满足：①在［a，b］连续；②在（a，b）可导；③f（a）=f（b），则在（a，b）至少存在一点ξ，使得f′（ξ）=0.

证明 若f（x）恒为常数，结论肯定成立.

若f（x）不恒为常数，由f（x）在［a，b］连续，f（x）在［a，b］存在最大值M，最小值m，且M≠m（若M=m，则f（x）恒为常数）.

且M，m至少有一个不为端点函数值，不妨设为M，即∃ξ∈（a，b），使得f（ξ）=M

∀x∈（a，b），f（x）≤f（ξ）=M

又f（x）在（a，b）可导，则f（x）在ξ处可导，由Fermat定理，有

f′（ξ）=0

定理中的三个条件缺一不可，否则结论不一定成立.例如，函数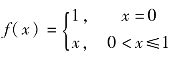，在［0，1］不连续，如图3.2所示；g（x）=，-1≤x≤1在（-1，1）不可导，如图3.3所示；h（x）=x，0≤x≤1在两端点函数值不等，如图3.4所示，它们都不满足罗尔定理的全部条件，也都不具有罗尔定理的结论.但要注意的是罗尔定理的条件仅是充分的，并不是必要的.也就是说，一个函数不满足罗尔定理的全部条件，也有可能在区间内部某一点的导数为零.

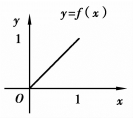
图3.2

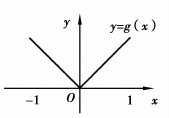
图3.3

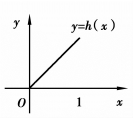
图3.4

例3.1 验证罗尔定理对于函数在区间［-1，1］上的正确性.

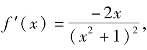证明 f（x）在［-1，1］上连续，在（-1，1）内可导，f（-1）=f（1）.故在［-1，1］上满足罗尔定理的条件，且取ξ=0∈（-1，1），有f′（ξ）=0，即罗尔定理成立.

例3.2 已知f（x）=1+xm（x-1）n（m，n都是正整数），证明方程f′（x）=0至少有一个不超过1的正根.

证明 由于f（x）=1+xm（x-1）n在［0，1］上连续，在（0，1）内可导，f（0）=f（1）=1.由罗尔定理，在（0，1）内至少存在一点ξ，使f′（ξ）=0，即x=ξ是f′（x）=0的根.

例3.3 若函数f（x）在［a，b］上连续，在（a，b）内可导，则存在ξ∈（a，b），使

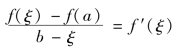
证明 设F（x）=xf（x）-xf（a）-bf（x），由已知，F（x）在［a，b］上连续，在（a，b）内可导，F（a）=F（b），所以存在ξ∈（a，b），使f′（ξ）=0.

又因为

F′（x）=f（x）+xf′（x）-f（a）-bf′（x）

故

F′（ξ）=f（ξ）+ξf′（ξ）-f（a）-bf′（ξ）=0

即

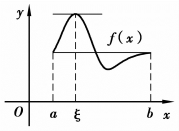
图3.5

罗尔定理的几何意义是：在闭区间［a，b］上有定义的连续曲线y=f（x），曲线上每一点都存在切线，在闭区间［a，b］的两个端点a与b的函数值相等，即f（a）=f（b），则曲线上至少有一点，过该点的切线平行于x轴，如图3.5所示.

罗尔定理还可以进一步推广，这就是下面的广义罗尔定理：

若函数f（x）满足在［a，+∞）可导则在（a，+∞）至少存在一点ξ，使得f′（ξ）=0.(www.xing528.com)

类似还可以写出其他形式的广义罗尔定理，证明也都是类似的.

（2）拉格朗日（Lagrange）中值定理

定理3.3 若函数f（x）满足：①在［a，b］连续；②在（a，b）可导，则在（a，b）内至少存在一点ξ，使得f（b）-f（a）=f′（ξ）（b-a）.

证明　令φ（x）=f（x）-由已知，φ（x）在［a，b］内连续，φ（x）在（a，b）内可导，且φ（a）=φ（b），由罗尔定理，至少∃一个ξ∈（a，b），使φ′（ξ）=0.

所以为函数曲线y=f（x）在［a，b］端点连线的斜率，f′（ξ）为曲线上（ξ，f（ξ））处切线的斜率.即在定理条件下，曲线上至少存在一点处的切线平行于端点连线，如图3.6所示.

f（b）-f（a）=f′（ξ）（b-a）

拉格朗日中值定理又称为微分中值定理、中值公式、拉格朗日公式.它还有不同的表达形式：

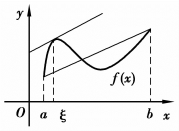
图3.6

拉格朗日中值定理的几何意义是明显的

由ξ∈（a，b），令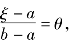有0＜θ＜1，ξ=a+θ（b-a），所以拉格朗日公式可以表示为

f（b）-f（a）=f′［a+θ（b-a）］·（b-a）

如果把［a，b］换成 [x，x+Δx]，拉格朗日公式可以表示为

f（x+Δx）-f（x）=f′（x+θ·Δx）·Δx（0＜θ＜1）

推论3.1 若f（x）在（a，b）内有f′（x）=0，则在（a，b）内f（x）恒为一常数.

推论3.2 若两函数f（x）及g（x）在（a，b）内成立f′（x）=g′（x），则在（a，b）内

f（x）=g（x）+c （c为一常数）

推论3.3 若f（x）在［a，b］上存在有界导数，则f（x）在［a，b］满足李普希兹（Lipschitz）条件：存在常数L＞0，使得对于［a，b］上任意两点x′，x″成立

例3.4 证明恒等式arcsinx+arccos

证明 令f（x）=arcsinx+arccosx

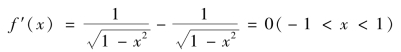
故

f（x）=c（-1＜x＜1）

而且所以

例3.5 证明不等式

证明 令f（z）=sinz，对任意x，y∈R，不妨设x＜y，则有f（z）在 [x，y]连续，在（x，y）可导.由拉格朗日中值定理，∃x＜ξ＜y，使得

所以