设y=f(x)是一个经济函数,其导数f′(x)称为y=f(x)的边际函数,f′(x0)称为f(x)在点x0的边际函数值.设f(x)在x0处有一个增量Δx,相应地,函数值有一个改变量Δy=f(x0+Δx)-f(x0).若f(x)在x0可微,则Δy≈f′(x0)Δx,特别地,当Δx=1时,Δy≈f′(x0).该式说明:自变量x在x0处改变“一个单位”时,函数y近似改变f′(x0)个单位,经济学中常略去“近似”而直接说改变了f′(x0)单位,这就是边际函数值的经济学意义.
例2.41 设y=2x2(图2.4),试求y在x=5时的边际函数值.
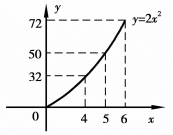
图2.4
解![]() 即当x=5时的边际函数值为20.其意义是:在x=5处x改变一个单位时,y改变20个单位,亦即x:5→6或5→4,y均改变了20(注意是近似值).把边际函数的概念具体应用到经济函数中产生了边际成本、边际收益、边际利润等概念.
即当x=5时的边际函数值为20.其意义是:在x=5处x改变一个单位时,y改变20个单位,亦即x:5→6或5→4,y均改变了20(注意是近似值).把边际函数的概念具体应用到经济函数中产生了边际成本、边际收益、边际利润等概念.
设成本是产量的函数C=C(q),则MC=C′(q)称为边际成本.MC的经济学意义是:在q0处,多生产一个单位产品或少生产一个单位产品所增加或减少的成本为C′(q0).
设收益是产量的函数R=R(q),则MR=R′(q)称为边际收益.MQ的经济学意义是:在q0处,多销售一个单位产品或少销售一个单位产品所增加或减少的收益为R′(q0).
设利润是产量的函数L=L(q),则ML=L′(q)称为边际利润.ML的经济学意义是:在q0处,多销售一个单位产品或少销售一个单位产品所增加或减少的利润为L′(q0).
例2.42 设C(q)=0.001q3-0.3q2+40q+100,求边际成本函数和q=50单位时的边际成本,并解释后者的经济学意义.
解 由于边际成本函数为MC=C′(q)=0.003q2-0.6q+40,于是q=50单位时的边际成本为![]() 其经济学意义为:生产第50个产品或第51个产品时,所花成本为17.5个单位.(https://www.xing528.com)
其经济学意义为:生产第50个产品或第51个产品时,所花成本为17.5个单位.(https://www.xing528.com)
事实上,生产第50个产品所花成本为C(50)-C(49)=17.65,生产第51个产品所花成本为C(51)-C(50)=17.351.
例2.43 设某产品的需求函数为![]() (p为价格,q为销售量),求销售量为15个单位时的总收益、平均收益与边际收益,并求当销售量从15个单位增加到20个单位时收益的平均变化率.
(p为价格,q为销售量),求销售量为15个单位时的总收益、平均收益与边际收益,并求当销售量从15个单位增加到20个单位时收益的平均变化率.
解 总收益为![]() ,故:
,故:
销售量为15个单位时的总收益R(15)=225;
销售量为15个单位时的平均收益![]()
销售量为15个单位时的边际收益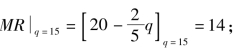
销售量从15个单位增加到20个单位时收益的平均变化率
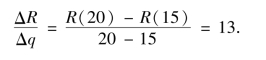
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




