高阶导数的求解方法及例题分析

设已知物体的运动方程为s=s（t），则物体的运动速度为v（t）=s′（t），而速度在时刻t0的变化率：

即在时刻t0的速度变化的快慢，这就是运动物体在时刻t0的加速度.加速度是速度函数的导数，也就是路程s（t）的导数的导数，这就产生了高阶导数的概念.

一般来说，对于函数y=f（x），其导函数f′（x）仍是x的函数.（f′（x））′（如果存在）就称为f（x）的二阶导数.记为：

类似地，二阶导数的导数称为三阶导数，三阶导数的导数称为四阶导数……，一般地，（n-1）阶导数的导数称为n阶导数.记为：

二阶及二阶以上的导数称为高阶导数.

求高阶导数就是多次连续地求导数，求导方法与求一阶导数一致.下面首先讲几个初等函数的n阶导数.

例2.32 求y=ex的n阶导数.

解 y′=ex，y″=ex，…，y（n）=ex，即

（ex）（n） =ex

例2.33 求y=sinx，y=cosx的n阶导数.

解 y=sinx

所以

类似y=cosx

例2.34 求y=xn的n阶导数.

一阶导数有运算法则，高阶导数同样存在着运算法则：

若函数u（x）、v（x）具有n阶导数，则

［u±v］（n） =u（n）±v（n）

对于乘法运算法则就比较复杂一些，两个函数相乘，求高阶导数，存在莱布尼兹公式

其中u（0）=u，v（0）=v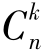，表示从n个不同元素中取出k个的组合数.

例2.36 设y=excosx，求y（5）.(www.xing528.com)

解 令u（x）=ex，v（x）=cosx

例2.37 研究函数

的高阶导数.

所以f′（x）在x=0不可导，即f（x）在x=0处二阶导数不存在.

综上所述：

f（n）（x）=0，x≠0，n＞2；f（n）（0）（n＞1）都不存在.

注意：对分段函数在各段分界点上的导数（包括高阶导数）都应由导数定义考察它的可导性.

下面对于参数方程所表示的函数，求其二阶导数

若φ，ψ在［a，b］上都是二阶可导，则由

对于复合函数，同样可求高阶导数.设z=g（y），y=f（x）都存在高阶导数，求复合函数z=g［f（x）］的高阶导数.

注意：复合函数关于中间变量求导数，所得到的仍然是中间变量的函数.例如上面复合函数z=g（y），y=f（x），运算过程中的就仍然是中间变量y的函数，中间变量y又是自变量x的函数，所以就仍然是自变量x的复合函数，求仍要用复合函数的求导法则，所以

例2.39 若f″（x）存在，求函数y=f（x2）的二阶导数

解

例2.40 求由隐函数ey-xy=0所确定函数的二阶导数

解 将y看作x的函数，应用复合函数求导法则，方程两边关于x求导有

于是

再对（*）式两端关于x求导，有

将代入即可得