高等数学-导数定义与几何意义

切线问题和速度问题都是描述当自变量发生变化时，函数变化的快慢.它们的数学形式也都是一致的，都是函数的改变量比上自变量的改变量，当自变量改变量趋于0时的极限.

这种具有特定意义的极限就称为函数的导数，也叫作函数的变化率.

定义2.1 设函数y=f（x）在x0附近有定义，对应于自变量的任一改变量Δx，函数的改变量Δy=f（x0+Δx）-f（x0），如果极限

存在，则此极限值就称为函数f（x）在x0处的导数（也叫微商），记为

这时也称f（x）在x0导数存在，或者f（x）在点x0可导.

类似地有左右导数的定义，若存在，则极限值就称为函数f（x）在x0处的右导数，记为f′+ (x )0 ；若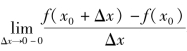存在，则极限值就称为函数f（x）在x0处的左导数，记为f′- (x )0 .

由极限存在的充要条件

所以

f′（x0）存在⇔f′+（x0），f′-（x0）存在且相等

这是函数f（x）在一点可导的概念.下面是函数f（x）在区间可导的概念：

若f（x）在（a，b）内每一点可导，则称f（x）在（a，b）可导.若f（x）在（a，b）可导，且f′+（a），f′-（b）存在，则称f（x）在［a，b］可导.

若f（x）在一个数集X上可导，即对X中每一点，有一个相应的导数值与之对应.由函数的概念，函数f（x）的导数就构成了X上的一个函数，这就是f（x）的导函数.(www.xing528.com)

注意：在上面式子中，虽然x可以取数集X上的任何数值，但在极限过程中，x是常量，Δx是变量.

函数f（x）在点x0处的导数f′（x0）就是导函数f′（x）在点x=x0处的导数值，即

导函数f′（x）简称导数.

至于导数的几何意义，在导数的引进中已经给出了实例.f′（x0）就是相应函数曲线y=f（x）在横坐标为x0处切线的斜率，即

f′（x0）=tanα

其中α是切线的倾角.

如果y=f（x）在点x0处的导数为无穷大，这时曲线y=f（x）的割线以垂直于x轴的直线x=x0为极限位置，即曲线y=f（x）在点M（x0，f（x0））处具有垂直于x轴的切线x=x0.

根据导数的几何意义并应用直线的点斜式方程，可知曲线y=f（x）在点M（x0，y0）处的切线方程为

y-y0 =f′（x0）（x-x0）

过切点M（x0，y0）且与切线垂直的直线叫作曲线y=f（x）在点M处的法线.如果f′（x0）≠0，法线的斜率为从而y=f（x）在点M处的法线方程为