【摘要】:由函数在一点x0连续的定义在x0要连续,必须满足:以上条件任何一个不满足,均会造成函数不连续,即间断.下面给出间断点的分类:关于第一类间断点,还可以细分:左右极限存在且相等,即存在,此时间断,要么f(x)在x0无定义;要么虽有定义,但.对于可去间断点,可补充函数在x0的定义或改变函数在x0的定义,使函数f(x)在x0连续.例1.57 指出函数的间断点,并判别其类型.解 函数在x=1处没有定义,所以
由函数在一点x0连续的定义![]() 在x0要连续,必须满足:
在x0要连续,必须满足:

以上条件任何一个不满足,均会造成函数不连续,即间断.
下面给出间断点的分类:

关于第一类间断点,还可以细分:
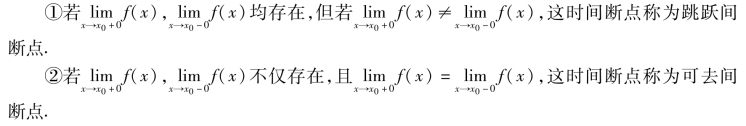
左右极限存在且相等,即![]() 存在,此时间断,要么f(x)在x0无定义;要么虽有定义,但
存在,此时间断,要么f(x)在x0无定义;要么虽有定义,但![]() .对于可去间断点,可补充函数在x0的定义或改变函数在x0的定义,使函数f(x)在x0连续.
.对于可去间断点,可补充函数在x0的定义或改变函数在x0的定义,使函数f(x)在x0连续.
例1.57 指出函数![]() 的间断点,并判别其类型.
的间断点,并判别其类型.
解 函数![]() 在x=1处没有定义,所以x=1为函数的间断点.因
在x=1处没有定义,所以x=1为函数的间断点.因
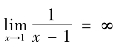
故x=1为函数的第二类间断点.我们也形象化地称x=1为![]() 的无穷间断点,如图1.22所示.
的无穷间断点,如图1.22所示.
例1.58 指出函数![]() 的间断点,并判别其类型.
的间断点,并判别其类型.
解 函数![]() 在点x=0没有定义;当x→0时,函数值在-1与+1之间变动无限多次,所以点x=0为函数的第二类间断点.我们也形象化地称为函数
在点x=0没有定义;当x→0时,函数值在-1与+1之间变动无限多次,所以点x=0为函数的第二类间断点.我们也形象化地称为函数![]() 的振荡间断点,如图1.23所示.
的振荡间断点,如图1.23所示.
例1.59 指出函数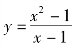 的间断点,并判别其类型.
的间断点,并判别其类型.
解 函数![]() 在点x=1没有定义,所以函数在点x=1为不连续.但这里(https://www.xing528.com)
在点x=1没有定义,所以函数在点x=1为不连续.但这里(https://www.xing528.com)
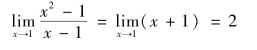
如果补充定义:令x=1时y=2,则所给函数在x=1成为连续.所以x=1称为该函数的可去间断点,如图1.24所示.
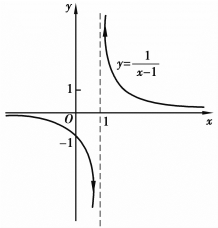
图1.22
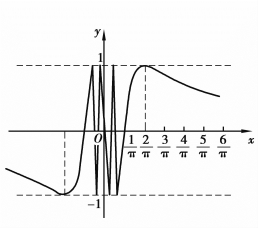
图1.23
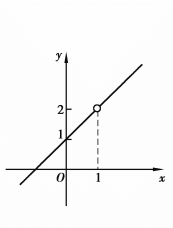
图1.24
例1.60 求函数![]() 的间断点和类型.
的间断点和类型.
解 函数![]() 在x=0,x=±1处没有定义.
在x=0,x=±1处没有定义.
x=0时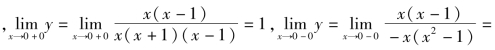 -1,x=0为第一类间断点.
-1,x=0为第一类间断点.
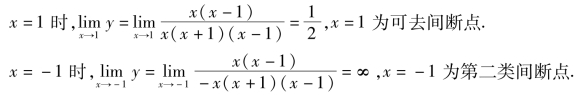
例1.61 令![]() 求f(x)的间断点和类型.
求f(x)的间断点和类型.
解 计算极限可得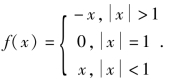
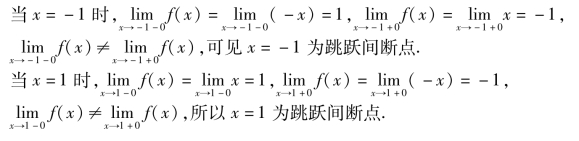
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




