《高数上2版》初等函数连续

初等函数是日常最为常见的函数，它连续与否？它在什么情形下连续？都直接影响着我们对问题的讨论和对结果的论证.

首先是基本初等函数的连续性.

（1）三角函数和反三角函数的连续性

前面用定义已经证明了sinx在（-∞，+∞）连续.

这是一个复合函数.里层函数在（-∞，+∞）连续，外层函数y=sinμ在（-∞，+∞）连续.由复合函数的连续性定理：

有

由连续函数的运算法则：连续函数之商在使分母不为0的点连续.分母不为0的点也就是这几个函数定义域上的点，所以这几个函数在其定义域上连续.

由此得到所有三角函数在其定义域上连续.

由连续函数的反函数定理，反三角函数也在其定义域上连续.

（2）指数函数和对数函数的连续性

对于指数函数y=ax，a＞0，a≠1，如图1.21所示。

设a＞1，首先证明ax在0点的连续性.

①设为某个正整数，由a＞1，有

图1.21

已知，又当n→∞时，得x→0+0，故

所以ax在0点右连续.

②再证明ax在0点左连续.

当x＜0，设x=-y，则且y＞0，有

所以ax在0点左连续.

综上所述，ax在0点连续.

下面证明ax（a＞1）在任何一点x0连续，由

(www.xing528.com)

已证ax在0点连续，得

当x→x0时，有

所以y=ax（a＞1）在任何一点x0连续，即在（-∞，+∞）连续.

又当0＜a＜1时，令，其中b＞1

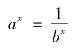
因bx在（-∞，+∞）内连续，由连续函数运算法则，得ax在（-∞，+∞）内连续，所以y=ax（a＞0，a≠1）在（-∞，+∞）内连续.

由反函数的连续性定理，其反函数对数函数

y=logax（a＞0，a≠1）

在（0，+∞）连续.

（3）幂函数的连续性

对于幂函数

y=xα

当x∈（0，+∞）时，有

xα =elnxα =eαlnx

lnx在（0，+∞）连续，eμ在（-∞，+∞）内连续，由复合函数的连续性定理：可知y=xα 在（0，+∞）内连续.

当x∈（-∞，0）时，只有α为整数或（n，m为整数）时，xα才有意义.已知xα在（0，+∞）连续，由xα的奇偶性，可推出其在（-∞，0）的连续性.

例如它在（0，+∞）上是连续的.它是一奇函数，由奇函数图像关于原点对称，所以它在（-∞，0）上也是连续的.

当x=0时，xα在α＞0时有意义，可由定义证明xα在0点连续.

（4）双曲函数的连续性

双曲函数由指数函数四则运算得到，而ex在（-∞，+∞）连续，所以由连续函数的运算法则，双曲函数在其定义域内连续.

由此可见：基本初等函数在其定义域内连续.

最后，由第一节中关于初等函数的定义，由基本初等函数的连续性以及连续函数的运算法则、复合函数的连续性定理，可得到下列重要结论：

一切初等函数在其定义域内都是连续的.

根据函数f（x）在点x0连续的定义，如果已知函数f（x）在点x0连续，那么求f（x）在x→x0的极限时，只要求出f（x）在x0的函数值即可.因此，上述关于初等函数连续性的结论提供了求极限的一个方法，这就是：如果f（x）是初等函数，且x0是f（x）定义域中的点，则

例如