在自变量的变化过程中,函数趋向于无穷大,就称函数在这一自变量的变化过程中为无穷大量.
随着自变量不同的变化过程,函数为无穷大量呈现不同的表现形式:
结合前面数列为无穷大量以及各种情况下函数极限的描述,可写出对应的定义.例如,f(x)→-∞(x→x0+0)⇔∀G>0,∃δ>0,当0<x-x0<δ时,有f(x)<-G.
和数列无穷大量一样,函数无穷大量也存在着类似的性质.
下面的性质中,记号“lim”下面没有标明自变量的变化过程.实际上,同一性质中自变量的变化过程为同一变化过程即可.
性质1.6 若limf(x)=∞,那么![]() 反过来,如果在向变量的变化过程中f(x)无零点,并且limf(x)=0,那么
反过来,如果在向变量的变化过程中f(x)无零点,并且limf(x)=0,那么![]()
性质1.7 若lim f(x)=∞,而g(x)在自变量的变化过程中![]() 那么limf(x)g(x)=∞.
那么limf(x)g(x)=∞.
例1.45 讨论
其中a0≠0,b0≠0,m和n为非负整数,并由此计算:
解 当m=n时,分子、分母各除以xn,得到
因为x→∞,由无穷大量与无穷小量的关系,得到![]() 再由函数极限的四则运算法则,可得
再由函数极限的四则运算法则,可得
当m>n时,用xm 除分子分母,和上面一样,有
当m<n时,由
得
综上所述,有
应用上面结果,可直接得到
例1.46 讨论函数![]() 在x=-1处的极限.
在x=-1处的极限.
解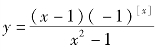 ,由于是讨论函数在x=-1处的极限,因此只需考虑x=-1邻近区域的函数值即可.(https://www.xing528.com)
,由于是讨论函数在x=-1处的极限,因此只需考虑x=-1邻近区域的函数值即可.(https://www.xing528.com)
当-2<x<-1时,[x]=-2,则
当-1<x<0时,[x]=-1,则
所以
例1.47 已知下列极限,确定a与b,使
分母x的最高次数为1次,要极限为0,由例1.45的讨论可知,分子x的最高次数必须低于1次,可得
解方程组,可得
将![]() 代入,极限
代入,极限![]() 不存在.所以
不存在.所以
例1.48 举出符合下列要求的函数f(x).
(1)f(+0)=0,f(-0)=1.
解 满足条件的函数可举出很多,例如
(2)f(+∞)=0,f(-∞)不存在.
解 f(x)=e-x,它满足
(3)f(x0+0)和f(x0-0)都不存在.
解![]() 它满足f(x0+0)和f(x0-0)都不存在.
它满足f(x0+0)和f(x0-0)都不存在.
(4)f(x0+0)=1,f(x0-0)=+∞
解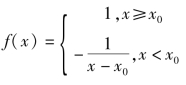
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




