高数上2版：无限远处的极限函数

前面讨论了当自变量趋于有限值时函数的极限.其实，还可以将函数极限的概念推广到自变量趋于无限的情形.

一般地，当自变量x的绝对值无限增大时，如果函数f（x）与常数A无限接近，则称x→∞时，f（x）的极限为A.

定义1.15 设函数f（x）在x的无穷远处有定义，设A为一个常数，若对任意给定的ε＞0，存在X＞0，当时，有

则称A是f（x）在无限远处的极限，或者说A是当x→∞时f（x）的极限.记为

这时也称函数f（x）在无限远处极限存在.

函数f（x）在x的无穷远处的极限定义可简写为A⇔∀ε＞0，∃X＞0，当时，有其几何解释如图1.19所示.

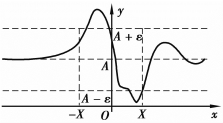
图1.19

当然x→∞有可能只向正的方向，也有可能只向负的方向.

函数在正无限远处极限的定义：

定义1.16 设函数f（x）在x的正的无穷远处有定义，设A为一个常数，若对任意给定的ε＞0，存在X＞0，当x＞X时，有

就称A是f（x）在正的无限远处的极限，或者说A是当x→+∞时f（x）的极限.记为(www.xing528.com)

这时也称函数f（x）在正的无限远处极限存在.

函数f（x）在x的正的无穷远处的极限定义可简写为

定义1.17 设A为一个常数，若对任意给定的ε＞0，存在X＞0，当x＜-X时，有

就称A是f（x）在负的无限远处的极限，或者说A是当x→-∞时f（x）的极限.记为

这时也称函数f（x）在负的无限远处极限存在.

函数f（x）在x的负的无穷远处的极限定义可简写为