高数上：函数在一点的极限为

极限是一种变化的趋势.如果一个函数y=f（x），其自变量x无限接近于一个确定的数值x0时，对应的函数值f（x）无限制地逼近一个确定的数值A，就称A是函数f（x）当x→x0时的极限.

要寻求x→x0时函数f（x）的变化趋势，首先必须保证f（x）在x0的去心邻域有定义.

在x→x0的过程中，对应的函数值无限地逼近A，也就意味着要多小就有多小.如同数列极限一样，要刻画要多小就有多小，就任给一要多小就有多小的正数ε，让小于这个要多小就有多小的正数，即

当然，f（x）无限制地逼近A，是在x趋近x0的过程中产生的.f（x）逼近A的程度不一样，所要求x趋近x0的程度也不一样，可用来刻画x趋近x0的程度.δ是某个正数，随ε的不同而不同.

意味着x可不等于x0.事实上，f（x）可在x0处无定义.

通过以上分析，下面给出x→x0时函数极限的定义.

定义1.14 设函数f（x）在x0 点的去心邻域有定义，又设A是一个定数.如果对于任意给定的ε＞0，一定存在δ＞0，使得当时，有

就称A是函数f（x）在x0点的极限，记为

这时也称函数f（x）在x0点收敛.否则称f（x）在x0点发散.

注意：

①定义中的δ依赖于ε，但又不是函数关系.一般说来，ε越小，相应的δ也越小.当δ找出后，任何δ0（0＜δ0＜δ）都可充当δ的角色.

②讨论x→x0时函数f（x）的极限，与函数f（x）在x0有无定义并无关系.不等式

就是限制x既要属于x0的δ邻域，又不等于x0.因此不能将其写成(www.xing528.com)

定义可以简单地表述为：

图1.16

下面给出函数f（x）当x→x0时的极限为A的几何解释（图1.16）：

与x0-δ＜x＜x0+δ，x≠x0等价.

即f（x）当x→x0时极限为A，意味着对任意ε＞0，总存在以x0为心、δ为半径的去心邻域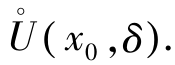.在此区域内，函数图像落在y=A-ε，y=A+ε两直线之间，或者说相应函数值落在以A为心、ε为半径的邻域之中，即

f（x）∈U（A，ε）

关于函数在一点的极限定义，与数列情况类似，可以写出它的一些等价定义.函数也有无穷小量的定义.在自变量的变化过程中，函数极限为0，函数称为在此自变量变化下的无穷小量.关于函数在一点的极限定义，也可以写出它的反定义.

下面用定义证明几个函数极限