如何用数学语言刻画数列的无穷大量

前面讲了数列的极限.随着n值的增大，数列无限制地逼近一个常数.

事实上，数列还有另外一种变化的趋势，随着n值的增大，数列无限制地增大，这就是无穷大量.

怎样用数学语言刻画数列无限制地增大呢？

任取一个要多大就有多大的正数G，让数列的绝对值来刻画数列｛xn｝无限制地增大.

同样，xn无限制地增大是随着n值的增大而产生的.增大程度不一样，所要求的n值也不一样，从而可得出无穷大量的定义.

定义1.13 设｛xn｝ 是一个数列，如果对任意给定的G＞0，总存在正整数N，当n＞N时，必有就称｛xn｝是一个无穷大量.记为：

或

xn→∞（n→∞）

事实上，数列是无穷大量表明数列不存在极限，写成或称数列的极限为∞，只是为了方便所作的形式上的一种表示.

注意：

①无穷大量不是很大的数.很大的数是一个常数，而无穷大量是一个变量.

②数列是无穷大量，则数列一定无界，反之不成立.即数列无界不一定是无穷大量.例如，｛n+（-1）nn｝无界，但不是无穷大量.

无穷大量的几何解释（图1.15）：

(https://www.xing528.com)

图1.15

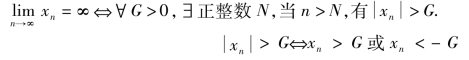
即｛xn｝是无穷大量，意味着任给G＞0，｛xn｝自某项之后一定落在

（-∞，-G）∪（G，+∞）

区域内.或者说：意味着∀G＞0，在［-G，G］只有｛xn｝的有限多项.

当然，对于无穷大量的定义，如同前面极限定义一样，可类似写出许多注意事项和等价定义.

下面来证明两个无穷大量.

例1.32 按定义证明下列数列为无穷大量：

∀G＞0，不妨设G＞1，取N=[ 2（G-1）] +1.当m＞N，n＞2m ＞2N 时，有

为无穷大量.

关于无穷大量，还可以进一步细化：正无穷大量，负无穷大量.