高等数学单调有界数列

在研究比较复杂的数列极限问题时，通常分两步来解决：先判断该数列是否有极限（极限的存在性问题）；若有极限，再考虑如何计算此极限（极限值的计算问题）.这是极限理论的两个基本问题.

为了确定某个数列是否有极限，当然不可能将每一个实数依定义一一加以验证，根本办法是直接从数列本身的特征来作出判断.

下面给出数列极限的一个判别定理：单调有界定理.

有界数列前面已经有定义，下面给出单调数列的概念：

定义1.9 若数列｛xn｝满足：

x1≤x2≤…≤xn≤xn+1…

则称该数列是单调增加的；若数列｛xn｝满足：

x1≥x2≥…≥xn≥xn+1…

则称该数列是单调减少的.若将式中的“≤”或者“≥”改为“＜”或者“＞”，则称数列｛xn｝是严格单调增加或者严格单调减少.

定理1.7（单调有界准则） 单调有界数列必有极限.

该定理说得具体一点，即：单调增加有上界的数列必有极限；单调减少有下界的数列必有极限.

这个结论在几何直观上看是显然的.从数轴上来看，单调递增数列｛xn｝只可能向右移动，故只有两种可能：①若｛xn｝无上界，则点xn沿数轴正向移向无穷远；②若｛xn｝有上界，则xn无限趋于某一个定点A，即xn→A（n→∞）.

图1.14

但几何直观不能代替严格的数学证明.为证明该定理，需要用到数集的上下确界的有关结论.

定义1.10（上确界） 给定一个实数集E，如果存在一个实数β，满足：

①∀x∈E，都有x≤β；

②∀ε＞0，∃y∈E，使得y＞β-ε；

则称β为数集E的上确界.记为β=supE.

上确界定义中的第一个条件说明β为数集E的一个上界；第二个条件说明β为数集E的最小的上界.

类似地可以定义一个数集的下确界：

定义1.11（下确界） 给定一个实数集E，如果存在一个实数α，满足：

①∀x∈E，都有x≥α；

②∀ε＞0，∃y∈E，使得y＜α+ε；

则称α为数集E的下确界.记为α=infE.

上确界定义中的第一个条件说明α为数集E的一个下界；第二个条件说明α为数集E的最大的下界.

上确界与下确界统称为确界.

定理1.8 若实数集E有上界，则E必有上确界；若实数集E有下界，则E必有下确界.

这就是确界原理，它可以作为一个公理加以应用.这个公理被称为极限理论的基石，是微积分理论最基础的东西.

下面就来证明单调有界数列的收敛性定理.这里只证明单调增加有上界的情形.

证明 数列｛xn｝的所有项构成一个数集E，由于数列｛xn｝有上界，故数集E有上界，所以也存在上确界.设数集E的上确界为A，于是∀ε＞0，∃xN∈｛xn｝，使得

xN ＞A-ε

又由数列｛xn｝单调增加有上界知，当n＞N时，有(www.xing528.com)

A+ε＞A≥xn≥xN ＞A-ε

故

由证明过程可以看出单调增加有上界数列收敛于该数列的最小的上界，即上确界.同样的，单调减少有下界数列收敛于该数列的最大的下界，即下确界.

要注意的是单调有界准则只是一个数列存在极限的充分性定理，反之并不成立，即收敛的数列不一定单调，如，但数列并不是单调的.

下面利用单调有界准则来讨论一个非常著名的极限，它也是微积分中非常重要的一个极限.

考察数列的极限，写出此数列的前几项，看一看它的规律：

从前几项可以看出该数列是单调增加的，且增加的速度很缓慢，但其极限肯定大于2.

下面就来严格证明此数列单调增加且有上界.由二项式定理得

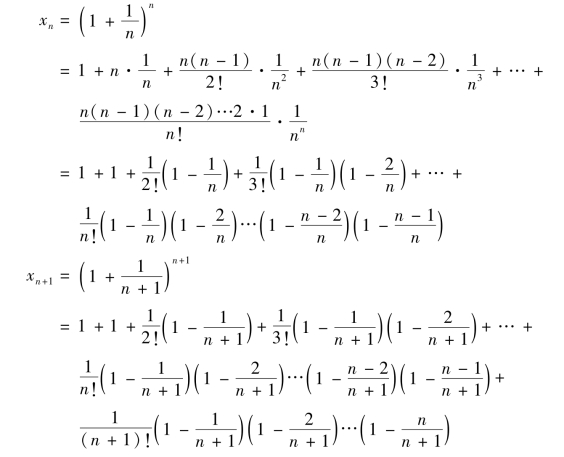
xn+1比xn多出一项：

另外，由于

故

xn ＜xn+1，n=1，2，3，…

即数列｛xn｝单调增加.下面证明这个数列有上界.由

这样就证明了数列单调增加且有上界，故存在.用字母e来表示这个极限，即

e是一个无理数，它就是自然对数的底数，e=2.71828….

数e和π是数学中应用最广泛的超越常数.e也可定义为

例1.29 证明：若｛xn｝单增，｛yn｝单减，而｛xn-yn｝极限为零，则｛xn｝和｛yn｝必有同一极限.

证明 已知｛xn-yn｝极限为零，所以｛xn-yn｝有界.存在A、B∈R，使得∀n

A≤xn-yn≤B

又｛xn｝上升，｛yn｝下降，所以

x1≤xn≤yn+B≤y1+B

y1≥yn≥xn-B≥x1-B

即｛xn｝、｛yn｝有界，故｛xn｝、｛yn｝均收敛，且