《高等数学：计算数列的极限》

数列极限的定义、数列极限的性质可以用来讨论数列的极限，但是要计算数列的极限，用得最多的还是数列极限的运算法则.

①若数列｛xn｝，｛yn｝都有收敛，则它们的和与差｛xn±yn｝也收敛.且有

证明 仅对差加以证明（和类似可证），设

由数列极限的定义，∀ε＞0，∃正整数N1，当n＞N1，有

∃正整数N2，当n＞N2，有

取N=max（N1，N2），当n＞N时，有

所以

特别地，无穷小量的和差仍为无穷小量.

②若｛xn｝，｛yn｝收敛，则｛xnyn｝也收敛，并且

证明 由已知数列｛xn｝，｛yn｝收敛，设

收敛数列有界，故∃M＞0，使得∀n，有

由xn→a，yn→b（n→∞），则∀ε＞0，∃正整数N1，当n＞N1，有

∃正整数N2，当n＞N2，有

取N=max（N1，N2），当n＞N时，有

所以

特别地，无穷小量的乘积仍为无穷小量.

③设｛xn｝为有界数列，｛yn｝极限为零，则它们的积｛xnyn｝极限为零.

证明 已知｛xn｝为有界数列，故∃M＞0，使得∀n，有

又｛yn｝为无穷小量，故∀ε＞0，∃正整数N，当n＞N，有

由数列极限的等价定义，则(www.xing528.com)

④若｛xn｝、｛yn｝都收敛，且，则也收敛，且.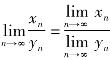

证明 由已知数列｛xn｝，｛yn｝收敛，设

由yn→b，故

由保号性，∃正整数N′，当n＞N′，有

又xn→a，yn→b（n→∞），则∀ε＞0，∃正整数N1，当n＞N1，有

∃正整数N2，当n＞N2，有

取N=max（N1，N2，N′），则当n＞N时，有

由数列极限的等价定义，则

注意，数列极限的和差、积的运算法则对于两个数列成立，事实上对于有限个都成立，对于无限多个不成立.

另外，数列极限和、差、积、商的运算法则，是在各个数列极限存在的前提条件下成立的，没有这个前提条件则不能使用.

例如就不能写成因为不存在.而应直接利用上面的第三个运算法则.它为一个无穷小量和一有界量的乘积，仍为一无穷小量.

例1.23 考察

其中k，l都是正整数，且k≤l，ai，bj（i=0，1，…，k；j=0，1，…，l）都是与n无关的数，a0≠0，b0≠0.

解 可改写：

应用和与差的运算法则，可得

再应用除法运算法则，得

而

于是根据乘法运算法则，得

再根据例1.23，有