上面给了极限的思想,那么如何用数学语言准确地描述极限呢?
首先如何用一个数学式子准确地刻画xn无限制地逼近常数a这个事实?一般来说:要描述两个数的相差程度,是用这两个数差的绝对值来描述的,所以xn与a的逼近程度一般用![]() 来衡量.但又怎么描述其逼近程度是无限制的呢?xn 无限制地向a逼近,也就是
来衡量.但又怎么描述其逼近程度是无限制的呢?xn 无限制地向a逼近,也就是![]() 要它有多小,它就有多小.就任意给定一个正数ε>0,要它有多小就有多小,让
要它有多小,它就有多小.就任意给定一个正数ε>0,要它有多小就有多小,让![]() <ε,这样来刻画xn与a无限制地逼近.
<ε,这样来刻画xn与a无限制地逼近.
当然,xn与a无限制地逼近是在n无限制地增大的情况下产生的.逼近程度不一样,所要求的n值也不一样.
例如![]() 当n→∞时,xn→1.
当n→∞时,xn→1.
令ε=0.01,![]() <0.01,n>100,即数列{xn}要逼近到与1相差小于0.01,只需从101项开始即可满足;令ε=0.001,
<0.01,n>100,即数列{xn}要逼近到与1相差小于0.01,只需从101项开始即可满足;令ε=0.001,![]() ,即数列{xn}要逼近到与1相差小于0.001,则需从1001项开始方可满足.
,即数列{xn}要逼近到与1相差小于0.001,则需从1001项开始方可满足.
由此得到刻画数列极限的定义.
定义1.6(数列极限的定义) 设{xn}是一个数列,a是实数.如果对任意给定的ε>0,总存在一个正整数N,当n>N时,都有![]() ,就称a是数列{xn}的极限,或者称数列{xn}收敛,且收敛于a,记为
,就称a是数列{xn}的极限,或者称数列{xn}收敛,且收敛于a,记为
![]()
若数列{xn}没有极限,则称这个数列不收敛,或称它为发散数列.
注意:
①在此定义中,ε的作用是衡量数列xn与其极限a的逼近程度,因此ε必须任意(当然这里应该说是任意小).
②并非要求所有xn都满足![]() ,而只要从某一项xN 以后的项都满足即可.至于这个N有多大,x1,x2,…,xN 这些项是否满足,不加过问.所以N不在大小,只须存在.
,而只要从某一项xN 以后的项都满足即可.至于这个N有多大,x1,x2,…,xN 这些项是否满足,不加过问.所以N不在大小,只须存在.
③ε给定在先,N找到在后,N依赖于ε,但它们之间的关系又不是函数关系.这是因为,ε给定后,只要能找到一个N,那么N+1,N+2,…都可以充当N的角色.
④根据ε的职能与特点,在证明有关极限问题时,往往把ε限制在某一个范围内.例如,∀ε>0,不妨设ε<α0(α0>0),若存在正整数N,当n>N时
![]()
这样一定对于任意不加限制的ε>0,也有
![]()
为了表达方便,引入记号“∀”表示“对于任意给定的”或“对于每一个”,记号“∃”表示“存在”.数列极限![]() 的定义可简写为
的定义可简写为
![]()
数列极限的几何解释:
由![]() 与a-ε<xn<a+ε等价.数列{xn}极限为a,意味着∀ε>0,总存在正整数N,数列{xn}在第N项以后,所有项xN+1,xN+2,…都夹在a-ε,a+ε之间.或者说在(a-ε,a+ε)以外最多只有x1,x2,…,xN 中的有限多项,如图1.13所示.
与a-ε<xn<a+ε等价.数列{xn}极限为a,意味着∀ε>0,总存在正整数N,数列{xn}在第N项以后,所有项xN+1,xN+2,…都夹在a-ε,a+ε之间.或者说在(a-ε,a+ε)以外最多只有x1,x2,…,xN 中的有限多项,如图1.13所示.
![]()
图1.13
数列极限的定义也可以用邻域来叙述:
![]()
下面再写出几个与极限定义等价的常用叙述:
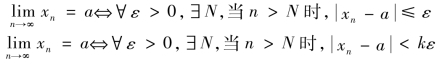
其中,k>0为常数
![]() (https://www.xing528.com)
(https://www.xing528.com)
![]() 只有数列{xn}的有限多项在U(a,ε)之外.
只有数列{xn}的有限多项在U(a,ε)之外.
若一个数列以0为极限,则此数列称为无穷小量.
关于数列极限与无穷小量的关系,下面给出一个重要的结论(函数极限与无穷小量具有类似的结论).这个结论在极限的讨论过程中经常会用到.
定理1.2 若一个数列存在极限,则此数列等于其极限加上一个无穷小量;反之,若一个数列等于一个确定的数加上一无穷小量,则此数列存在极限,且极限就是这一确定的数.
证明 若一个数列存在极限,设![]() 由极限的定义,∀ε>0,∃正整数N,当n>N时,有
由极限的定义,∀ε>0,∃正整数N,当n>N时,有
![]()
令xn-a=αn,则
![]()
由数列极限的定义,即数列{αn}为无穷小量,且
![]()
反之,若一个数列等于一个确定的数加上一无穷小量,设xn=a+αn,其中αn→0(n→∞).由极限的定义,∀ε>0,∃正整数N,当n>N时,有
![]()
又xn-a=αn,则
![]()
即
![]()
另外,由数列极限的定义,数列极限存在与否只与数列在后面无穷多项的值有关.一个数列、去掉、添加或改变它的有限个项的数值,不改变其敛散性与极限值.
数列极限的定义是一种非构造性的定义.具体来说,该定义只给出一个数列{xn}与一个常数a是否有极限关系的“定性”描述,并未给出由已知数列求出其极限的具体方法.因此,在用极限定义讨论有关极限问题时,必须预先知道其极限,否则就不能用.因此,极限定义一般用作证明极限问题.


证明 反推可证明不等式:
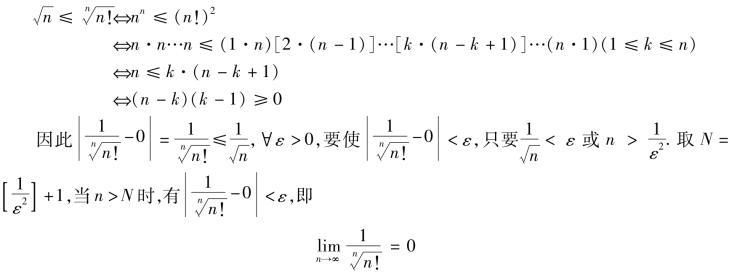
此外,还可以利用数列极限的定义证明数列不存在极限,即利用它的反定义.下面写出数列极限的反定义.
![]()
另外,数列{xn}不存在极限⇔即任何有限数均不是{xn}的极限⇔∀a∈R,∃ε0>0,∀N,∃n0>N,有![]() .
.
例1.17 证明数列![]() 发散.
发散.
分析:即要证明,∀a∈R,∃ε0>0,∀N,∃n0>N,有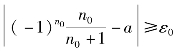 .
.
证明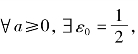 ∀N,∃n0=2k+1>N,有
∀N,∃n0=2k+1>N,有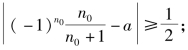 ∀a<0,∃ε0=
∀a<0,∃ε0=![]() 有
有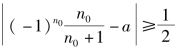 ,所以
,所以![]() 发散.
发散.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




