定义1.4 函数y=φ(u)的定义域为U,而函数u=f(x)的定义域为X,值域为U*.若U∩U*≠∅,那么对于X内相应x,经过中间变量u,得到唯一确定的一个值y.于是y经过中间变量u而成为x的函数,记为
y=φ(f(x))
这种函数称为复合函数.其中,y=φ(u)称为外层函数,u=f(x)称为内层函数.
注意,两个函数通过中间变量,要构成复合函数,只需内层函数的值域与外层函数的定义域交集非空,即U∩U*≠∅.内层函数的值域包含于外层函数的定义域只是其特殊情形.
复合函数定义域是内层函数定义域的子集,复合函数值域是外层函数值域的子集.
例如,外层函数为![]() ;内层函数为u=1-x2,X=(-∞,+∞),U* =(-∞,1];U∩U* =[0,+∞)∩(-∞,1]=[0,1]≠∅,所以可以构成复合函数
;内层函数为u=1-x2,X=(-∞,+∞),U* =(-∞,1];U∩U* =[0,+∞)∩(-∞,1]=[0,1]≠∅,所以可以构成复合函数![]() 定义域为[-1,1]⊂(-∞,+∞).
定义域为[-1,1]⊂(-∞,+∞).
若U∩U* =∅,则不能构成复合函数,φ(f(x))没有意义.
例如,y=arcsinu,U=[-1,1];u=2+x2,X=(-∞,+∞),U* =[2,+∞),U∩U* =[-1,1]∩[2,+∞)=∅,所以不能构成复合函数.(https://www.xing528.com)
实际问题当中也可能遇到两个以上函数所构成的复合函数,只要它们顺次满足构成复合函数的条件即可.
例1.9 已知f(2x-1)=x2,x∈R,求函数f(f(x))的值域.
解 f(f(x))是一个复合函数,可看成由y=f(u),u=f(x)复合而成,首先必须求出f(x)的表达式,由f(2x-1)=x2,x∈R,令2x-1=u,则![]() ,有
,有
可复合
定义域为(-∞,+∞),值域为![]() .
.
例1.10 设![]() 求f(g(x)).
求f(g(x)).
解 f(g(x))=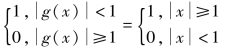
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




