在实际问题当中，通常存在两类不同性质的量.一类是在事物的发展变化过程中保持不变的量，这种量称为常量.一类是在事物的发展变化过程中会起变化的量，这种量称为变量.
在同一事物的发展变化过程中，变量不会孤立地存在.不同的变量之间相互依赖、相互联系、相互作用，把这种关系抽象出来，就是函数关系.
定义1.1 如果对某个范围X内的每一个实数x，按照某个对应法则f，得到Y内唯一实数y和这个x相对应，就称f是X上的函数，它在x的数值（称为函数值）是y，记为f（x），即y=f（x）.y是x的象，x是y的逆象，记为
f：X→Y或x→f（x）
X是定义域.所有f（x）的全体，即｛f（x）|x∈X｝为值域.
这个定义的核心是“对应法则f是X上的函数”，而y=f（x）是x所对应的函数值.它把函数和函数值严格予以区分.但为了叙述方便，习惯上仍常用记号“f（x），x∈X”或“y=f（x），x∈X”来表示定义在X上的函数，这时应理解为由它所确定的函数f.
表示函数的记号是可以任意选取的，除了常用的f外，还可使用其他的英文字母或希腊字母，如“g”“F”“φ”等.相应地，函数可记作y=g（x），y=F（x），y=φ（x）等.有时还直接用因变量的记号来表示函数，即把函数记作y=y（x）.但在同一个问题中，讨论到几个不同的函数时，为了表示区别，需用不同的记号来表示它们.
函数是从实数集到实数集的映射，其值域总在R内.因此构成函数的要素是：定义域X及对应法则f.如果两个函数的定义域相同，对应法则也相同，那么这两个函数就是相同的，否则就是不同的.
例1.1 函数
这两个函数对应法则相同，但定义域不同，它们是两个不同的函数.
例1.2 函数
这两个函数尽管对应法则的表达形式不同，但对应法则本质是相同的，定义域也相同，它们是两个相同的函数.
函数的定义域通常按以下两种情形来确定：一种是对于有实际背景的函数，根据实际背景中变量的实际意义确定.例如，在自由落体运动中，设物体下落的时间为t，下落的距离为s，开始下落的时刻t=0，落地的时刻t=T，则s与t之间的函数关系是
这个函数的定义域就是区间［0，T］；另一种是对于抽象地用算式表达的函数，通常约定这种函数的定义域是使得算式有意义的一切实数组成的集合.
例1.3 求下列函数的定义域：
（1）y=
解 这是一个分式函数，要使算式有意义，
即x＜0，所以定义域为｛x|x＜0，x∈R｝.
（2）y=
解 这是一个对数函数，要使算式有意义
，且x≠0，则
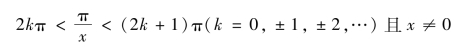
即
（k=±1，±2，…）或x＞1，定义域为
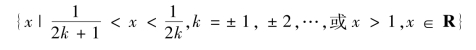
在函数的定义中，要特别注意其中“唯一”两字.对每个x∈X，对应的函数值y总是唯一的，它是决定一个实际问题中是否能构成函数关系的关键.
例1.4 设正方形的周长集合是A，对应规律f是“由正方形的周长x∈A到正方形的面积y”，问f是否是定义在A上的函数？
解 任意正方形的周长x∈A，相应正方形边长为
对应规律f使x对应该正方形唯一的面积
即f是定义在A上的函数.
例1.5 设三角形的周长集合是A，对应规律f是“由三角形的周长x∈A到三角形的面积y”，问f是否是定义在A上的函数？
解 任取三角形的周长x∈A，设三角形三边之长分别是a，b，c，即a+b+c=x，对应规律f使x对应该三角形的面积
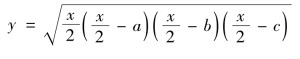
当给定x时，a、b、c都可进行变化，即对应规律使x对应的三角形面积y不是唯一的，不满足函数的定义，所以f不是A上的函数.
在函数的定义中，对每个x∈X，对应的函数值y总是唯一的，这样的函数有时被称为单值函数.事实上，我们常常遇到这种情形，对每个x∈X，对应的函数值y总是确定的，但并不唯一，这样的函数称为多值函数.对于多值函数，往往需要将其转化为单值函数，再进行讨论.例如，x和y的关系式由方程x2+y2=1给出，对于每一个x∈［-1，1］，都有确定的y值与之对应.当x=-1，1时，对应的y值唯一；当x∈（-1，1）时，每一个x对应的y值有两个.可以将其转化为两个单值函数进行讨论，即
和
无特别说明时，本书所说的函数均指单值函数.(www.xing528.com)
表示函数的主要方法有3种：表格法、图形法、解析法（公式法）.其中，用图形法表示函数是基于函数图形的概念，即坐标平面上的点集
称为函数y=f（x），x∈X的图形.
（1）几个比较特殊的函数
1）分段函数
有些函数在其定义域的不同部分用不同的公式表达，这类函数称为分段函数.
2）符号函数
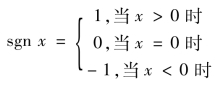
如图1.3所示，符号函数有一个比较重要的等式：
3）最大整数函数
这个函数可用一句话来表达：y是x的最大整数部分.换一句话说，y是小于或等于x的最大整数.如图1.4所示，例如，［1.5］=1，［1］=1，［-1.5］=-2.
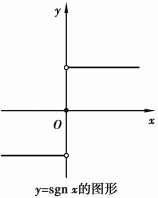
图1.3
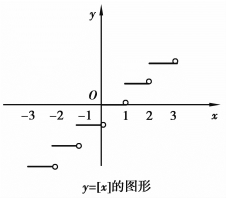
图1.4
4）狄立克莱（Dirichlet）函数
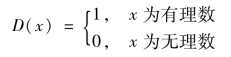
5）黎曼（Rimann）函数
（2）函数的四则运算
给定两个函数f（x），x∈D1；g（x），x∈D2.记D=D1∩D2，并设D≠∅，定义f（x）与g（x）在D上的和、差、积运算如下：
F（x）=f（x）+g（x），x∈D
G（x）=f（x）-g（x），x∈D
H（x）=f（x）g（x），x∈D
若在D中除去使g（x）=0的值，即令D0=D\｛x|g（x）=0，x∈D2｝≠∅，可在D0上定义f（x）与g（x）的商运算如下：
注意：①若D=D1∩D2=∅，则f（x）与g（x）不能进行四则运算.
例如，f（x）=arcsinx，x∈
；g（x）=
由于D=D1∩D2=∅，故f（x）与g（x）不能作四则运算.
②为叙述方便，函数f（x）与g（x）的和、差、积、商常分别写为：
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
