通过上述的讨论和例子，我们看到了规划求解的设计目标：基于一定的数据关系，在诸多约束条件下，实现某一控制目标，并查找出某些基础的管理控制数据。
我们也了解了规划求解的基本方法为：问题建模—量化约束与目标—求解。
现实工作中的数据关系可能更为复杂，约束条件也更多，如何利用规划求解获得最佳答案呢？这里以一个较为复杂的仓储物流优化问题来体会规划求解所具有的魅力。
随着经济的不断发展，特别是网络经济的兴起，仓储物流成为了企业乃至整个社会经济运行的一个重要支撑。如图17-72所示，假设一家公司在北京、上海、广州都有仓库，并且，从这些仓库到全国各地的运费各不相同。例如，北京仓到华北的运费单价为320元，而上海仓和广州仓到华北的运费单价分别为460元和530元，等等。现在，公司某个时段的运输量在第二张表格中被列出。其中：
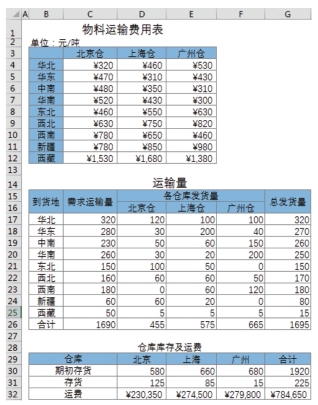
图17-72 规划求解—复杂问题模型
需求运输量：C17:C25为各个到货地所需要的货物运输量，即运算需求。
各仓库发货量：D17:F25为各个仓库往全国各地的发货量，这是调度需要参考的数据，也是规划求解可以优化的数据。图17-72表中的数据是人工调度根据直觉作出的安排。可以看到，手工作出的调度安排不仅数量存在一定的错误，而且运费合计多半不是最优的！
总发货量：为各个仓库向到货地发货的数量之和。因此，单元格G17的值为“=SUM(D17:F17)”，向下填充到G25。
最后一行“合计”为各项运输量之和、各项发货量之和，即单元格C26为“=SUM(C17:C25)”。计算出结果后，向右填充到G26。第三张表为仓库库存及运费，其中：
期初存货：为各个仓库的存货量，需要手工输入。
存货：为运输任务结束后仓库的存货，在数值关系上，为期初库存数据减去运输量合计数据，即D31单元格为“=D30-D26”，计算出结果后，向右填充到F31。因此，必须保证这些值不小于零。否则，这个运输安排中的某个仓库就会面临无货可发的窘境。
运费：为运输量与单价的乘积。这里由于各个仓库到各地的运费单价各不相同，因此，这个运费是用每个仓库发往各地的运输量乘以对应的运费，再求和算出来的。其算法在Excel中即为两个区域（矩阵）的相乘求和函数SUMPRODUCT( )，则D32单元格为“=SUMPRODUCT(C4:C12，D17:D25)”。计算出结果后，向右填充到F32。
最后一列“合计”即期初库存、存货和运费的合计，G30单元格为“=SUM(D30:F30)”。计算出结果后，向下填充到G32。
这里的G32单元格就是本次运输任务的最终运输费用合计，也是我们所要控制的目标。即通过合理规划，保证运费合计最低。至此，我们可以将整个问题表述为：在保证各个仓库有货可运的前提下，如何规划各个仓库到各地的发货量，使最终的运费合计最低？
操作步骤
【Step 1】 问题建模。按照问题的需求建立图17-72中的三张数据关系表格。(www.xing528.com)
【Step 2】 列出约束条件。根据上述说明，目标及所有约束为：
目标：G32最小。
约束：D31:F31区域中的各单元格值不小于零。G17:G25区域各单元格对应等于C17:C25区域的各单元格。
【Step 3】 实施规划求解。在规划求解功能已经被加载的情况下，单击“数据”选项卡—“分析”组—“规划求解” 按钮，启动如图17-73所示“规划求解参数”对话框。
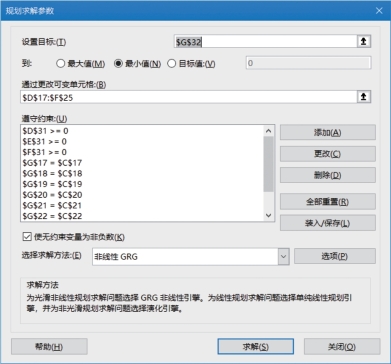
图17-73 规划求解参数配置
对设置目标（$G$32，最小值）、可变单元格（这里直接选择$D$17:$F$25区域）以及约束条件进行设置。然后，单击“求解”按钮，即可获得规划求解得出的最佳解，如图17-74所示。可以看到，Excel不仅对“各仓库发货量”的数据进行了优化，而且总发货量的错漏也被更正了。最关键的是，总运费明显降低了！
说明：
从运费最小化的目标看，规划求解得出的结果更符合逻辑。例如，华北地区全部由“北京仓”供货。
这一例子实际上还可进一步实用化，例如，加入在途运输量的参数、对仓库库存动态的考虑量等。
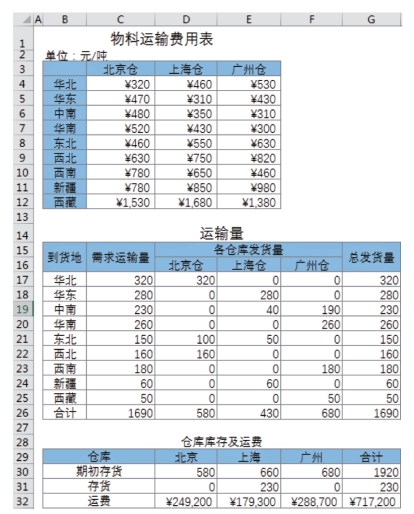
图17-74 规划求解的最佳解
图17-74中显示的结果为运用“单纯线性规划”求解方法所求得的结果。如果采用“非线性GRG”求解方法，得出的各项结果基本相同，只是广州仓的存货变为了“-2.65E-07”，即一个趋于零的很小的数。
【Step 4】 如果需要，还可以形成运算结果报告。
从这个例子中可以看出，规划求解的确是在一些复杂约束下求出问题最佳解的利器。我们还可以用它解决工作中的各种复杂问题，例如投资组合分析、生产配料优化、资源分配等，甚至可以用于求解多元方程组。
上例给出的规划求解参见本书提供的样例文档“仓储物流优化问题—规划求解.xlsx”。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
