数值信息的计算机表示方法

计算机主要通过数值计算来处理各种信息。因此，数值在计算机中的表示形式、存储格式、计算方法等，都是非常重要的基本技术。

1.常用数制的基本概念

数制也称计数制，是用一组固定的符号和统一的规则来表示数值的方法。与数制有关的概念包括数码、基数、位权及运算规则。

数码是数制中表示基本数值大小的不同数字符号。例如，十进制有10个数码：0、1、2、3、4、5、6、7、8、9。

基数是数制所使用数码的个数。例如，二进制的基数为2，十进制的基数为10。

位权是数制中某一位上的1所表示数值的大小（所处位置的价值）。例如，十进制的123，1的位权是100，2的位权是10，3的位权是1。

运算规则规定了数制计数时进位或借位的方法。例如，十进制的计数规则为“逢十进一，借一当十”。

1）十进制数

十进制有0、1、2、……、9共10个数码，运算规则是“逢十进一，借一当十”。

在计算机科学中，为了便于区分，十进制数用下标10或在数字尾部加D（Decimal）表示，如：（25）10、［25］10或23D。

各个数码的位权是由其所在的数位决定的。如图1-12所示，将小数点前一位的位号记为0，然后向左递增、向右递减，标记各位的位号，各数位的位权即为10的位号次方。

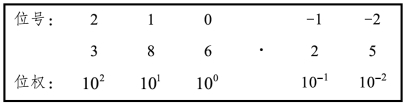
图1-12　十进制数386.25的位号与位权

【例1】将十进制数386.25按位权展开方式表示。

386.25D=3×102+8×101+6×100+2×10-1+5×10-2

2）二进制数

二进制只有0和1两个数码，运算规则是“逢二进一，借一当二”。在计算机科学中，二进制数用下标2或在数字尾部加B（Binary）表示，如：（1001）2、［1001］2或1001B。

二进制的计算法则与十进制基本相同，四则运算法则如下：

（1）加法：0+0=0，0+1=1，1+0=1，1+1=10（有进位）。

（2）减法：0-0=0，1-0=1，1-1=0，10-1=1（有借位）。

（3）乘法：0×0=0，0×1=0，1×0=0，1×1=1。

（4）除法：0÷1=0，1÷1=1（除数不可为0）。

二进制中各数码的权值与十进制类似，如图1-13所示。

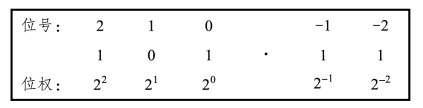
图1-13　二进制数（101.11）2的位号与位权

【例2】将二进制数101.11按位权展开表示。

101.11B=1×22+0×21+1×20+1×2-1+1×2-2

=1×22+1×20+1×2-1+1×2-2

3）十六进制数和八进制数

用二进制表示一个大数时，位数太多，人们很难辨认和记忆。因此，在计算机科学中经常采用十六进制数来表示二进制数，也有个别情况下使用八进制数来表示二进制数。特别需要注意，计算机内部并不采用十六进制数进行运算，引入十六进制数的原因是计算机专业人员可以很方便地在十进制和八进制、十六进制数之间进行转换。

十六进制的数码包括0～9十个数字和A、B、C、D、E、F六个字母，共16个数码。运算规则是“逢十六进一，借一当十六”。十六进制数用下标16或在数字尾部加H（Hexadecimal）表示，如，（2A）16、［2A］16或2AH。事实上，受C语言的影响，在计算机领域，更多时候使用前置“0x”的形式来表示十六进制数，如：0xA（或0x0000000A）表示十六进制数AH。

八进制的数码包括0～7八个数码，运算法则是“逢八进一、借一当八”。在计算机科学中，八进制数用下标8或在数字尾部加O（Octal，为与数字0区分，通常将O改写为Q），如：（127）8、［127］8或127O、127Q。

4）任意进制数的表示方法

设某进制数的基数为R（R≥2），则该数为R进制数，共有R个数码，运算规则为“逢R进一，借一当R”。

R进制数的位号与位权的关系如图1-14所示。对任意R进制的数，都可以用下列公式展开。

（An…A2A1A0.A-1A-2…A-m）R=AnRn+…+A2R2+A1R1+A0R0+A-1R-1+A-2R-2+…+A-mR-m

其中，Ai为数码，R为基数，n、m为数的位数（整数为0～n位，小数为-1～-m位）。

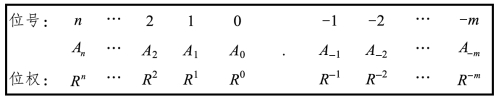
图1-14 R进制数的位号与位权

【例3】将八进制数47.25按位权展开表示。

47.25Q=4×81+7×80+2×8-1+5×8-2

【例4】将十六进制数4D.5A按位权展开表示。

4D.5AH=4×161+13×160+5×16-1+10×16-2(www.xing528.com)

2.不同数制的转换方法

在计算机科学中，经常使用到的数制包括十进制、二进制、八进制和十六进制。其中，人类使用最广泛的是十进制；计算机唯一能直接处理的数制是二进制；而八进制和十六进制则是计算机专业人员为更方便地使用二进制而引进的。因此，我们可以按角色总结出几种常用数制的转换法则，如图1-15所示。

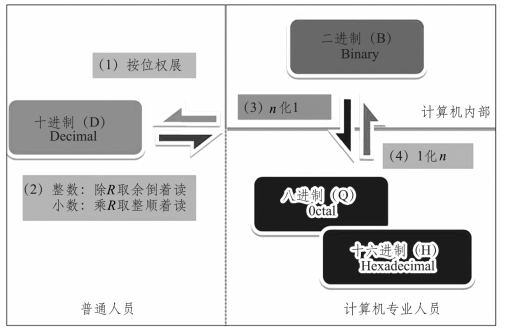
图1-15　数制转换速记图

1）其他数制转换成十进制

其他数制转换成十进制，按位权展开，并按十进制法则计算出结果即可。

【例5】将二进制数11010.01B转换为十进制数。

11010.01B=1×24+1×23+0×22+1×21+0×20+0×2-1+1×2-2

=16+8+2+0.25

=26.25D

从例5不难看出，二进制转换成十进制，只要将数码为1的位权相加即可。表1-3给出了2的整数次幂与其十进制数值的对应关系。

表1-3　2的整数次幂与其十进制数值的对应关系

【例6】将十六进制数A0B.CH转换为十进制数。

A0B.CH=10×162+11×160+12×16-1

=2560+11+0.75

=2571.75D

2）十进制转换成其他数制

将十进制转换成其他数制（R进制）时，整数部分和小数部分必须分开处理。

整数部分的转换法则为“除R取余倒着读”。具体方法为：使用短除法，用基数R去除十进制数，将余数记录在商的右边；若商不为0，再用基数R去除，记录余数，直到商为0；按从下到上的顺序，倒着读取每次记录的余数，即为整数部分转换结果。

小数部分的转换法则为“乘R取整顺着读”。具体方法为：使用乘法算式，用基数R去乘小数部分，计算完成后，将整数部分取出，记录在乘积的右边；若乘积不为0，再用基数R去乘，取走整数部分，直到乘积为0或满足转换精度的要求为止；按从上到下的顺序，顺着读取每次记录的整数，即为小数部分转换结果。

【例7】将十进制数57.375D转换成二进制数。

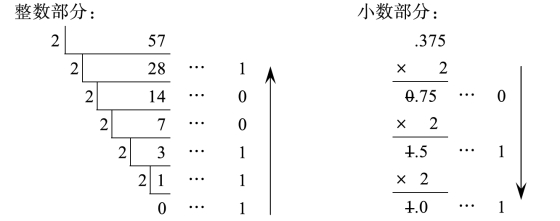
57.375D=111001.011B

【例8】将十进制数257.45D转换成八进制数。

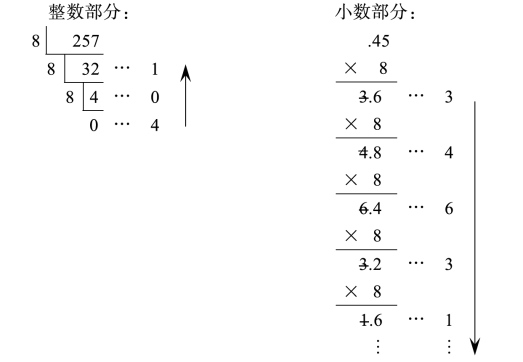
257.45D≈401.34631Q

特别注意，将十进制数转换成其他数制时，一个有限小数转换数制后可能是无限小数。

3）二进制转换成八进制或十六进制

二进制转换成八进制或十六进制的法则为“n化1”，即n位二进制化为1位八进制或十六进制。对于八进制，有23=8，故n=3，即3位化1位八进制数；对于十六进制，有24=16，故n=4，即4位化1位十六进制数。具体方法为：从小数点开始，分别向左、向右n位分为一组，当不足n位时，用0补足。分好组后，将每组独立地转换成目标数制即可。

【例9】将二进制数10110101.11B转换成八进制数。

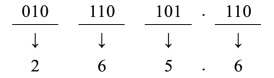
10110101.11B=265.6Q

【例10】将二进制数10110101.11B转换成十六进制数。

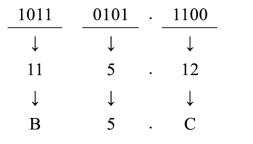
10110101.11B=B5.CH

4）八进制或十六进制转换成二进制

八进制或十六进制转换成二进制的法则为“1化n”，即1位八进制或十六进制化为n位二进制。对于八进制，n=3，即1位八进制数化3位二进制数；对于十六进制，n=4，即1位十六进制数化4位二进制数。

具体方法为：直接将八进制或十六进制数的各个数码转换为二进制数，然后按数码顺序将转换后的二进制数连接起来，去除首尾无效0即可。

【例11】将十六进制数B5.CH转换成二进制数。

B5.CH=10110101.11B