非饱和土壤墒情监测预报技术

饱和土壤的达西定律是人们所熟知的，它自1856年提出以来已有150多年了。对于一维情形，饱和土壤的达西定律可表为

式中 v——沿x方向的渗流速度；

Ψ——饱和土壤总土水势；

Ks——饱和水力传导度，又称渗透系数；

x——渗流方向上的距离。

实验与理论均证明，式（2-26）存在一个适用范围。当较小或太大时，由于v与的关系均为非线性关系，故式（2-25）不适用。只有当不太小也不太大时，式（2-26）才是适用的。

控制非饱和土壤水流运动的因素与控制饱和土壤水流运动的因素有所不同。一是两者总势的组成不同。在饱和土壤中，总势由重力势和静水压力势组成，而在非饱和土壤中，总势则由重力势和基模势组成。二是两者的水力传导度不同。饱和水力传导度是一个常数，非饱和水力传导度是土壤含水量的函数。干燥土壤的水力传导度最小，随着土壤含水量的增加，水力传导度也增加。当土壤含水量达到饱和时，水力传导度也达到最大，此即为饱和水力传导度。

水力传导度之所以随土壤含水量的增加而增加，原因主要有三（见图2-7）：一是由于土壤未达到饱和含水量之前，有些孔隙含有空气，减少了土壤横断面上的导水部分；二是由于吸力增加过程中，最初被抽空的孔隙是最大的那些，这样留给水分流动的只有较小的孔隙了；三是由于随着土壤含水量的减小，孔隙所形成的水流路径的弯曲度将有所增加。

图2-7　土壤水在孔隙中的运动

（a）饱和流；（b）非饱和流

现有的知识还不能建立起水力传导度与土壤含水量的理论关系。一些学者在实际工作中曾提出了一些经验公式，常见的形式有

式中 K——水力传导度；

θ——土壤含水率；(www.xing528.com)

α、m1——经验常数。

虽然非饱和水流与饱和水流具有以上不同的特点，但理查兹（Richards）于1931年用实验证明，非饱和水流也符合达西定律，即非饱和水流的渗流速度与总土水势梯度成正比，且与土壤中孔隙通道的几何性质有关。因此，对于非饱和水流，达西定律可表为

式中 v——非饱和土壤的渗流速度；

Ψ——非饱和土壤的总土水势；

K（θ）——非饱和土壤的水力传导度。

如将式（2-28）推广到三维情况，且只考虑x、y、z三个主方向上的各向异性，则有

式中 vx、vy、vz——x、y、z方向上的非饱和土壤的渗流速度；

Kx（θ）、Ky（θ）、Kz（θ）——x、y、z方向上的非饱和土壤的水力传导度；

其余符号意义同前。

当Kx（θ）=Ky（θ）=Kz（θ）=K（θ），即为各向同性土壤时，式（2-29）可简化为

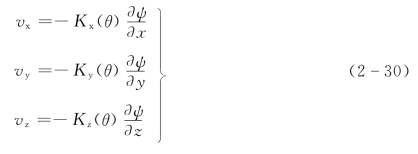
式（2-30）的向量形式为