德尔布吕克模型的讨论与验证：第五章成果

通过上面的事实，我们可以简单回答一个问题：数量不多的原子组成的结构——这样的遗传物质能否在漫长的时间中不受无时无刻不在发生的热运动干扰？我们应该假设基因的结构是一个巨大的分子，只会发生不连续的变化，这些变化主要是原子进行重新排列，最终产生同分异构体。

原子的重新排列可能只会影响到基因的一小部分区域，但是也可能有很多种不同的重新排列方式。由于能量阈的存在，分子的实际构型不会自发转变为任何一种同分异构体的构型，所以能量阈必须要足够高（与原子的平均热能相比），才能让自发转变成为小概率事件。这些小概率事件就等同于自发突变。

本章后面的内容会通过与遗传学事实进行详细对比，检验关于基因和突变的总体描述（主要理论来源是德国物理学家德尔布吕克）。

在对比之前，我们最好对该理论的基础和一般性质进行评述。

对生物学问题追根溯源，从量子力学的角度去回答问题是绝对必要的吗？我敢说，基因是一个分子这种推测在今天已经是老生常谈了。无论懂不懂量子理论，几乎没有生物学家会反对这一点。在第四章一开头，我们借经典物理学家之口说出了这种观点，因为只有这样才能合理解释我们观察到的持久性。接下来我们还提到了同分异构现象、阈能量、W/kT在决定同分异构体之间相互转化的可能性中的重要作用。以上所有内容我们都能够在不引入量子理论的情况下，纯粹以经验进行解释。

通过这本小册子我很难将量子力学解释得清清楚楚，也许还会让一大批读者感到无聊乏味，那我为什么还要强烈坚持用量子力学的理论解释这些问题呢？

量子力学是第一个能够从基本原理的角度解释我们在自然界中遇到的所有类型原子集合体的理论。海特勒-伦敦键是这一理论的独特的产物，其本来目的并不是解释化合键。这个理论成果的诞生过程非常有趣且令人费解，而我们出于完全不同的理由被迫接受了它。它完全符合我们观察到的化学现象，正如我所说，这是一个独有的特征，而且我们对它的理解足够深入，可以肯定地说，这样的事情在量子理论的未来发展中不可能再出现了。

因此我们可以断言，不存在其他的遗传物质的分子解释。从物理学领域来说，不可能有其他能解释遗传物质及其稳定性的可能了。如果德尔布吕克对遗传物质的描述是错误的，我们就得放弃进一步探讨的尝试了。这是我要说明的第一点。

但可能有人会问：是否除了分子之外，不可能存在其他由原子组成的稳定结构呢？比如，金币不是也能埋在墓穴当中数千年，其轮廓和表面的人物像依然清晰可见？金币的确是由无数原子构成的，但是我们不能将其外形保持良好归因于原子的大数规律。同样的理由也适用于我们从岩石当中找到的形状整齐的水晶，它们也经历了许多地质时期却没有发生变化。

这就引出了我想说明的第二点。无论是分子还是固态晶体，它们没什么不同。从现有的知识来看，从本质上讲它们是一样的。但不幸的是，学校教育还秉持着一些传统观点，这些观点已经过时了许多年，而且会妨碍人们对真实情况的理解。

的确，我们在学校习得的关于分子的内容并不会让我们觉得，相比于液态或气态物质，它们更接近固态物质的性质。相反，学校里学到的知识会让我们认真区分这些物理状态的变化，比如熔化或蒸发，在这些过程中分子本身是不会发生变化（比如，以酒精为例，无论是固体、液体，还是气体状态，酒精的分子永远都是C₂H₆O），而如果发生化学变化，比如酒精的燃烧，酒精分子会和3个氧气分子发生原子重新排列，形成2个二氧化碳分子和3个水分子，化学反应式为：

C₂H₆O+3O₂=2CO₂+3H₂O

至于晶体，我们在学校学过它们能够形成具有三维周期的晶格，在这样的晶格中有时候可以识别出单个分子的结构，比如酒精以及大多数有机化合物。而其他晶体，比如食盐（氯化钠，NaCl），情况则不太一样。氯化钠分子是无法被清晰地识别出来的，因为每个钠原子周围都对称地分布着6个氯原子，反之亦然，所以我们可以随便说哪个钠原子和氯原子是一对，可以组成氯化钠分子。

最后，我们还学过，固体可能是晶体也可能不是，对于后者我们会称其为无定形固体。

现在我不会非常极端地说，上述所有说法和区分都是错误的。从实际操作的角度而言，它们有时候还是有用的。但是讨论到物质真正的结构时，我们就要采取完全不同的方式划分物质的不同状态。下面两行“等式”可以表明两种区分方法之间的关系：

分子=固体=晶体
气体=液体=无定形固体

我们必须首先简单解释一下这些说法。所谓的无定形固体并不是真的没有形状，也不一定是固体。通过X射线，我们在“无定形”的碳纤维当中发现了石墨晶体的基本结构。所以木炭既是固体也是晶体。如果我们在一种物质当中找不到晶体结构，我们就得把它看作一种“黏性”（内部摩擦力）非常大的液体。这样的物质特征是没有明确的熔点，也不存在熔化潜热，所以并不是真正的固体。当你加热这种物质的时候，它会逐渐变软，连续变化，最终彻底成为液体（我记得，第一次世界大战快结束的时候，我们在维也纳时，被分配了一种沥青一样的物质代替咖啡。那东西太硬了，人必须得用凿子或斧头才能把小砖块一样的东西敲成小块碎片，裂开的地方非常光滑，像贝壳一样。但是，给它足够的时间，它就会表现出液体的性质，如果你用这种东西把容器底部塞满，并把它这样放上几天，你肯定会后悔）。

气态和液态的连续变化性质我们已经很熟悉了。只要靠近所谓的临界点，气体就会连续地液化。在这里我们就不多谈了。

我们已经证明了上面等式中的大部分内容，但还剩下关键的一点：我们希望能够将分子看作一种固体，也就是一种晶体。

原因在于，构成分子的原子无论多少，把它们凝聚在一起的作用力和无数原子构成真正的固体也就是晶体所使用的作用力，在本质上是完全一样的。分子能够展现出晶体一样的结构稳定性。

我们解释基因稳定性时所提到的恰好就是这样的稳定性！

物质结构中真正重要的区别在于，使原子结合在一起的是不是海特勒-伦敦键。对于固体和分子来说，原子都是由这种作用力结合在一起的。但是单个原子构成的气体（比如水银蒸汽），原子和原子之间的作用力就不是海特勒-伦敦键。分子构成的气体中，只有每个分子中的原子靠这种方式连在一起。

一个小分子可以被称为“固体的种子”。

从这样一个小小的种子开始，有两种方式能够让固体的规模逐渐变大。第一种方式比较无趣，就是向三个方向不断重复同样的结构，晶体的生长就是遵循这种方式。一旦周期确定了，规模的增长其实是没有明确上限的。

另一种方式是，不按照固定模式不断地重复。越来越复杂的有机分子就是采用这种方法。这样的分子中，每个原子、每个原子团都有各自的功能，和很多其他原子或原子团并不一样（而周期结构中则是一样的）。我们可以把这些分子称为非周期性晶体或固体，并且可以这样表达我们的假说：我们认为基因——或者整个染色体纤维——是一种非周期性固体。

人们经常会问，像受精卵的细胞核中这一点点物质，怎么可能包含着如此详细的代码文本，蕴含着未来生物发育的全部信息。

这似乎是我们唯一能够想到的物质结构：原子有秩序地排列在一起，并且有足够的抵抗力维持其秩序的稳定性，可以产生多种可能的（“同分异构”）排列方式，使其足以在狭小空间范围内承载一个复杂的“决定因素”系统。(www.xing528.com)

事实上，这样的结构中并不需要数量庞大的原子就能产生近乎无限可能的排列方式。以莫尔斯电码为例。这种电码由点和短线两种符号有规律地排列在一起，只用不超过4个这样的符号就能产生30多种不同的电码。如果你在其中加入点和短线之外的第三种符号，一串密码只要使用不超过10个符号，你就能拼出88572个不同的“词”；如果使用5种符号，密码不超过25位，你就能得到372529029846191405种不同的电码。你可能会说这种比喻说服力不够，因为我们的莫尔斯符号可以有不同的组合（比如“.—”和“. —.”），因此这不能与同分异构现象相对应。为了修正这种缺陷，我们从第三个例子中选出刚好25位的密码，并且每个密码都含有5种符号各5个（5个点、5个短线，以此类推）。粗略算一下大概能产生超过62330000000000个组合，确切数字算出来太麻烦，所以我就四舍五入到了百亿位。

当然，一方面，在实际情况中，并非原子的“每一种”排列方式都能构成一个分子，而且由于代码文本自身也要在发育过程中发挥执行作用，所以也不是任意一个密码都能当代码使用。

但另一方面，上述例子中的密码位数（25）其实是比较小的，而且我们这里使用的还只是简单的直线排列方式。我们只是希望证明，如果将基因描绘成分子，那么微型代码完全可以无比精确地编码极其复杂、特殊的发育计划，而且还能囊括这些计划的执行方案。

现在，我们终于可以开始将理论描述和生物学事实作比较了。

显然，我们要对比的第一个问题就是，理论描述是否能够真正解释我们所观察到的高度稳定性？为了获得这种稳定性所需的阈值——数倍于平均热能kT——是否合理？它们是否在普通化学所知的范围内？这个问题很容易解决，不需要查阅表格我们就能给出肯定的回答。化学家在特定温度下分离出来的任何物质的分子，在这一温度下都至少能够存在几分钟。这当然是保守的说法，一般来说，物质分子的寿命要长得多。因此，化学家遇到的阈值必然和解释生物学家面对遗传物质的稳定度所需要的数量级是吻合的。之前在“数学表达公式”一节中我们提到过，阈值的变化范围大约是1:2，阈值相对应的寿命大约是几分之一秒到数万年。

但是为了便于后面讨论引用，我需要在此提出一些数字。

在“分子的稳定性与温度有关”一节中，我们提出过一些W/kT的例子，也就是这一比例分别为30、50和60的情况下，分子的寿命分别是1/10秒、16个月和30000年，分别对应室温下0.9电子伏、1.5电子伏和1.8电子伏的阈值。

我们必须解释一下“电子伏”这个单位，对物理学家来说，用这个单位非常方便，因为你能对它进行视觉化想象。

举例来说，第三个数字（1.8电子伏）意味着一个电子经过大约2伏特电压的加速，会获得足够的能量撞击分子引起跃迁（为了便于比较，普通手电电池的电压是3伏特）。

由于这些原因，通过振动能的随机波动导致分子某些部分发生同分异构体的构型变化，实际上发生的概率足够小，完全可以将其理解为自发突变。

所以我们通过量子力学的原理就能够解释突变当中最惊人的事实了，这也是德弗里斯最初关注的东西。这个事实就是：突变是“跃迁”式的变化，没有任何中间形式出现。

我们发现，任何种类的电离辐射都会提高自然突变率，有的人可能会将自然突变率归因于土壤、空气中的放射性和宇宙辐射。但是与X射线实验结果进行对比就会发现，“自然辐射”过于微弱，只是造成自然突变率的很小一部分原因。

假设我们必须要用热运动的随机波动来解释自然突变，我们就不会惊讶于大自然成功地选择了这样精妙的阈值，使突变的发生这么罕见。因为从前面的内容当中，我们已经得到了结论，频繁的突变对演化是不利的。通过突变获得了不够稳定的基因构型的个体，很难有机会看到其“极端激进地”快速突变的后代长久生存下去。这个物种就会抛弃这些个体，并通过自然选择获得稳定的基因。

但是，对于繁育实验中出现的突变体和我们选择出的用于研究其后代的突变体，我们没有理由指望它们表现出极高的稳定性。因为它们并没有经过大自然的“洗礼”，如果把它们放在野生环境下自行繁育，可能就会由于更容易突变而被“淘汰”。无论如何，我们也不会惊异于一些突变体比正常的“野生”基因型具有更高的突变可能性。

所以，我们能够对突变性方程进行检验，方程如下：

t=τ×e^W/kT

（提醒一下，t表示突变发生的期待时间，W代表发生突变所需的阈能量。）

我们的疑问是，温度会如何影响t的变化？根据上面的方程，我们能够推导出温度为T+10和温度为T两种情况下，t的比值的近似方程为：

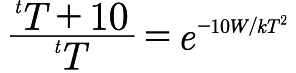
这个公式中指数已经变成负的了，所以，这个比例一定是小于1的。温度升高的情况下，期待时间也会相应降低，突变发生的概率也会增加。我们可以对这个假说进行验证，而且我们已经在果蝇这种昆虫可承受的温度范围内进行了验证。而验证结果乍看起来有点出乎意料。野生基因较低的突变率有了显著的提高，但是一些已突变基因的突变率却没有明显提高。如果我们对两个公式进行比较，这个结果就符合我们的预期了。根据第一个公式，对于稳定基因来说，W/kT的数值更大，这样期待时间才会更长，而根据第二个方程，W/kT数值更大也就导致比例数值较小，也就是说温度升高导致的突变性提高更明显。（实际情况中，这个比例的数值一般是1/5到1/2之间，其倒数在2-5之间，刚好是普通化学反应中所说的范托夫因子）

现在我们来讨论X射线的诱导突变率，根据繁育实验可以推断出两个结论。第一，（从突变率和辐射剂量的比例关系来看）突变是单一事件导致的结果；第二，（从定量结果和突变率是由整体电离密度决定的，而与辐射的波长无关的事实来看），导致突变的单一事件应该是电离或类似的过程，它必须发生在产生特定突变位置附近10个原子距离为边长的立方体空间范围内。根据我们的描述，用于达到阈值的能量明显必须由电离或激发这样的爆炸式过程所提供。我之所以说这些过程像爆炸，是因为一次电离过程所需的能量（这一能量并不是X射线本身所需要的，而是次级电子产生所需的）相当惊人，可达30电子伏。这一巨大能量能够转变为放电点周围急剧增强的热运动，并通过“热波”——原子剧烈振动形成的波——的形式传播出去。这种热波能够为10个原子距离空间的“作用范围”提供达到1-2个电子伏的阈能，这没什么不可思议的，虽然公平一点的物理学家可能会认为作用范围会小一点。

在很多情况下，这种爆炸的作用并不会让染色体发生有序的同分异构体转变，而会造成染色体损伤。当损伤的染色体在巧妙的互换作用下，替代了未受损伤的染色体（另一个染色体组当中相应的染色体）中的正常部分时，染色体的损伤就可能致命。所有这些都是可能发生的，而且已经被我们观察到了。

有很多特性虽然不能从我们对遗传物质的描述中直接预测出来，不过也很容易被理解。比如，总体来说，不稳定突变体的X射线诱导突变率并没有显著高于稳定突变体。因为，如果一次爆炸能够提供30电子伏的能量，你当然不会认为突变需要的阈值能量高一点低一点——比如1电子伏还是1.3电子伏——会有什么区别。

有些情况中跃迁是双向的，比如某种“野生”基因可以变成特定的突变基因，同时还可以从突变基因变回野生基因。这两种情况的自然突变率有时候几乎一样，有时候则完全不同。乍看起来这让人很困惑，因为这两种情况下要达到的阈值能量是一样的。但是要知道，变化所需要的能量还与初始构型的能量水平有关，而野生型基因和突变型基因在这方面可能并不一样。（见“第二个修正”一节图12，状态1可能代表野生等位基因，2代表突变等位基因，箭头更短代表的稳定性更低。）

整体而言，我认为德尔布吕克的“模型”是能够经得起事实检验的，我们可以在进一步的讨论中合理使用这一模型。