定量化学分析：相关系数与γ检验法优势

前面叙述回归线时以光度分析为例,溶液浓度与吸光度之间存在严密的直线关系。在实际工作中,只有当y 和x 之间存在着某种线性关系时,配出的直线才有意义,判断回归线是否有意义,主要靠专业知识,但在数学上可以借引入一个叫相关系数的量来定量地进行判断。用γ表示,γ的物理意义如图9-22所示。

从图9-22可看出,γ的绝对值愈接近1,x 和y 之间的线性关系愈好。如果接近于零,可认为x 和y 之间没有线性关系,如图9-22中的（c）、（d）两种情况。对上述计算的实例γ为：

图9-22 相关系数γ的意义

说明测定值均落在直线附近,两变量存在着定量关系。

相关系数γ的物理意义：

（1）当｜γ｜=1,所有的点都落在一条直线即回归直线上,此时称x 与y 完全线性相关,图9-22（a）及（f）即是。(www.xing528.com)

（2）当0＜｜γ｜＜1,这是绝大多数的情况,x 与y 之间存在一定的线性关系。当γ＞0时,y 有随x 增加而增大的趋势,此时称y 与x 正相关,图9-22（b）。当γ＜0时,y 有随x 增加而减小的趋势,此时称y 与x 负相关。

（3）当γ=0时,Lxy=0,即根据最小二乘法确定的回归直线平行于x 轴,图9-22（c）。说明y 的变化与x 无关,实验点的分布是不规则的,此时x 与y 毫无线性关系。因此图9-22（c）的回归直线是没有意义的。

由此可见,相关系数γ确实可以表示两个变量x 与y 之间线性相关的密切程度。｜γ｜愈接近1,y 与x 之间的线性相关就愈密切。这里需要指出的是：相关系数γ 所表示的两个变量之间的相关是指线性相关。因此,当γ很小甚至等于0时,并不一定表示x 与y 之间就不存在其他关系。例如图9-22（d）虽然γ=0,但从图上可看出x 与y 之间存在着明显的关系,只不过这种关系不是线性而已,从图9-22（d）看来,y 和x 之间很像存在着抛物线类型的曲线关系。

判断变量x 与y 是否存在线性关系,或者说线性关系好与不好是相对的。表9-7列出不同置信水平下的相关系数,用以检验线性关系。

表9-7 相关系数检验表

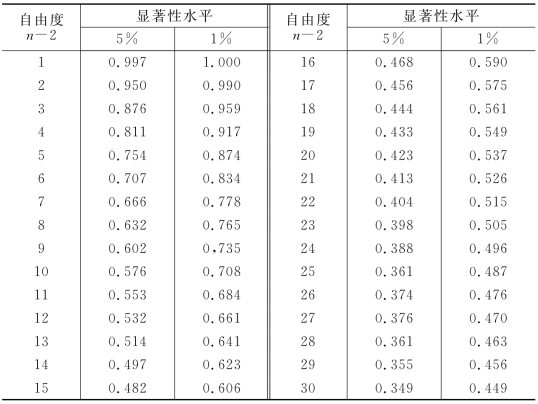
如果计算的γ值大于表中γα,f值,则表示在显著性水平为α时,y 与x 两个变量之间是显著相关的,即求得的回归关系是有意义的。若计算的γ值小于表中γα,f值,则γ不显著,此时x与y为线性不相关,在此情况下配回归直线就没有什么意义。在回归分析中,f=n-2。