准确滴定：终点误差判断

1.误差公式和误差图

表5-5 Δp M＇与f=10ΔpM＇-10-ΔpM＇换算表

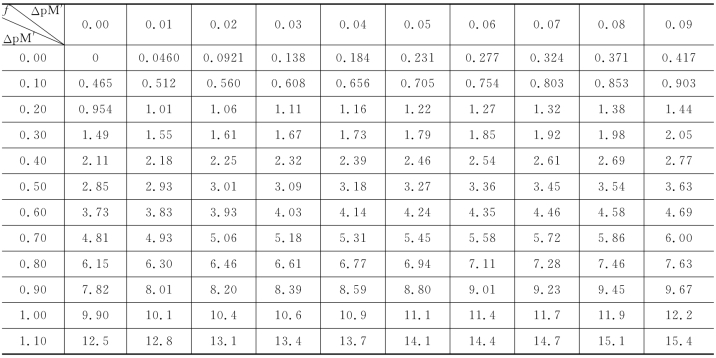
续表

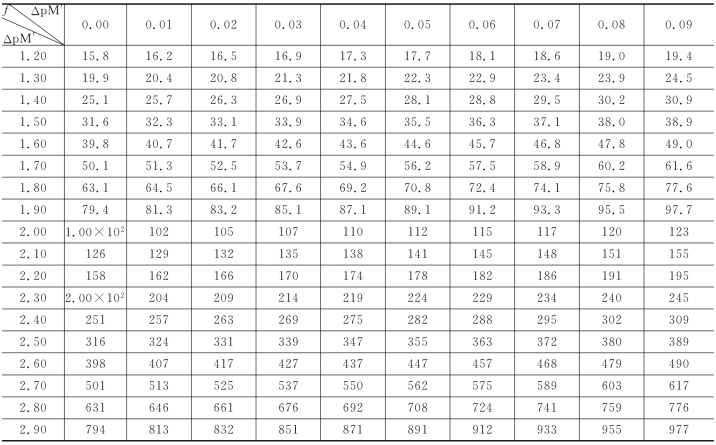
换算示例：①已知Δp M′=0.32,查Δp M′=0.30与0.02,得f=1.61；②已知f=-1.11,查Δp M=-（0.20+0.03）=-0.23。

将式（5-16-c）取对数,得

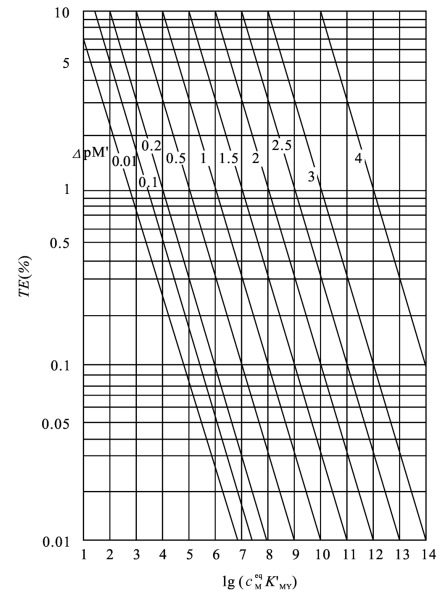
图5-10 滴定误差图

f=1.26,查表5-4得Δp Mg′=0.26

sp±0.1%处的p Mg′分别为5.1-0.26=4.84 和5.1+0.26=5.36。滴定突跃Δp Mg′（突）=0.26×2=0.52。

用相同方法可计算当TE=±0.2%时Δp Mg′=0.46,即终点与计量点的p M′之差为0.46单位。所谓“目视法”即指用指示剂确定终点的方法。由于人的生理局限性所致,在确定滴定终点时一般有±0.2～0.5p M 单位的不确定性,换言之,只有当p M 改变±（0.2～0.5）个p M 单位时人们才能确认出指示剂颜色的变化。可见该例中所述的滴定,用目视法确定终点可以满足误差在±0.2%范围之内的要求。

【例5-6】在pH=5.0的缓冲液中,用2×10-2 mol/L EDTA 滴定2×10-2 mol/L Cd2+,用二甲酚橙作指示剂,求

（1）变色点时终点误差；(www.xing528.com)

（2）若确定终点时还有±0.5p M 单位出入时的终点误差。

解 已知lg KCdY=16.5,pH=5.0时lgαY（H）=6.6,p Cdt（Cd-XO）=4.5。

lg KCdY′=lg KCdY-lgαY（H）=16.5-6.6=9.9

查误差图得TE=-0.1%。

可见滴定Pb2+时,应选用六次甲基四胺作缓冲溶液。

2.准确滴定的判断

能满足指定误差要求的滴定可称为“准确滴定”。如终点误差要求TE=±0.1%时,凡终点误差在-0.1%～0.1%范围内的滴定都属准确滴定。

表5-6 单一离子准确滴定的判据

通常也将｜TE｜≤0.1%,Δp M′=±0.2,cM=2×10-2 mol/L 称为一般条件。由表5-7可见,在一般条件下只有当才能被准确滴定。

表5-7 某些条件下(lg KMY＇ )ct值