精密度表示方法-《定量化学分析》

1.平均偏差、相对平均偏差

在相同条件下,用同一方法对某试样重复测定n次,得一组测量值x1,x2,…,xn。这些测量值的算术平均值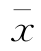 称为样本平均值。

任何一个个别测量值（或称单次测量值）与平均值之差称为该次测量的绝对偏差,用d表示：

di=xi-x-（3-5）式中i为1～n的正整数。

绝对偏差可正,可负,亦可为零,但一组数据中各单次测量值的绝对偏差之和一定为零。

将式（3-4）代入上式得：

单次测量值的绝对偏差在平均值中所占的百分数称为相对偏差,用dri表示：

绝对偏差及相对偏差只能评价相应的单次测量值与平均值之间的偏离程度,不能表示一组测量值（整个样本）中各测量值间的分散程度,即不能评价精密度,测定结果的精密度用平均偏差、相对平均偏差和标准偏差、相对标准偏差来衡量。

平均偏差：将各单次测量值的绝对偏差的绝对值进行算术平均,所得平均值称做平均偏差,用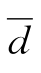 表示：

相对平均偏差：平均偏差在测量值的平均值中所占的百分数称为相对平均偏差,用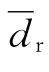表示：

平均偏差是以算术平均值的方式“统计”了各单次测量值的偏差,因此它在一定程度上可以反映一组测量值的精密度。这种方法虽然较简单,但存在不足之处。因为在多次测定所得的数据中,小偏差的测定总是占多数,大偏差的测定总是占少数,如果按总的测定次数计算平均偏差,所得结果会偏小,大的偏差在平均偏差中得不到反映。因此,在数理统计中常用标准偏差或相对标准偏差来表示精密度。

2.标准偏差、相对标准偏差

总体标准偏差：在无系统误差的前提下,无限次平行测定的结果x1,x2,…,xn（n→∞）组成一个总体,总体的平均值μ 可视为真值,因此单次测量值的偏差可视为误差,即E=xi-μ。将各次测量值的误差经平方后求得的算术平均值称为总体方差,用σ2 表示：

总体方差开平方并取正根,称为总体标准偏差,用σ表示：(www.xing528.com)

样本标准偏差：对于有限次测量来说,一组测量值的方差称为样本方差,用s2 表示：

相对应的标准偏差称为样本标准偏差,用s表示：

式中（n-1）在数理统计中称为自由度,说明在n次测定中,只有n-1个可变的偏差。

当时,自由度,所以

一般当n＞20时,s与σ 之间的差距就已经很小了。

相对标准偏差：标准偏差在平均值中占有的百分数称为相对标准偏差,用RSD 表示：

以前经常把相对标准偏差称为变异系数（简称为CV）,但现在已基本不用。

标准偏差与平均偏差有两点不同。其一是计算时不必考虑偏差的正负；其二是由于偏差的平方运算增强了大偏差数据的作用。因此,标准偏差比平均偏差更能灵敏地反映出数据的离散程度,较好地反映一组测定数据的精密度。

3.极差、相对极差

为了简便起见,有时也用极差来粗略估计一组平行测定数据的离散程度。极差也叫全距或范围误差,它是一组平行测定数据中的最大值与最小值之差,用R 表示：

相对极差：极差在平均值中占有的百分数,用Rr表示：

当测定次数n≤10时,标准偏差和极差间存在如下关系：

其中,C 是一随n 而变化的常数,具体数值可从有关的统计书中查到。在粗略计算时C 可取为测定次数的平方根,即：C=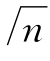。因此,可用下式估算标准偏差：