PAC编程实例：实用算术指令

我们介绍两个现场实例，来使用算术指令编写梯级逻辑。

我曾经到过一个自来水厂，那里的操作工抱怨他们的每日产量记录不准确。我调看了一段流量积累的例程，梯级逻辑自然是编得没有道理。我借用这个实例，编写了一个用算术指令处理的例程，作为教学使用，在这里跟大家分享一下。

实例的需求是：

一个采集流量的传感器，按吨/小时采集，传感器提供的是模拟量信号，且不管它是电流信号还是电压信号，作为精度足够高的模/数转换，我们得到的模拟量输入数据至少是千位数的，如果定标太低，精度就牺牲太多了。现在，我们要将这个采集到的数据进行累积，以得到每天流出自来水厂的总量，也即自来水的产量。

首先要分析的是每隔多长时间采集一次数据可以保证积累正确，有关人员提供了可靠的依据，对水量来说，1s采集1次数据足以保证精确。现在我们用一个计时器就可以解决问题了，每秒钟产生一个动作脉冲，如图6-7所示。Logix控制器的计时精度足够满足这个需求，如果要求更紧密、更精确的时间采集，我们只好求助于定时中断任务了。

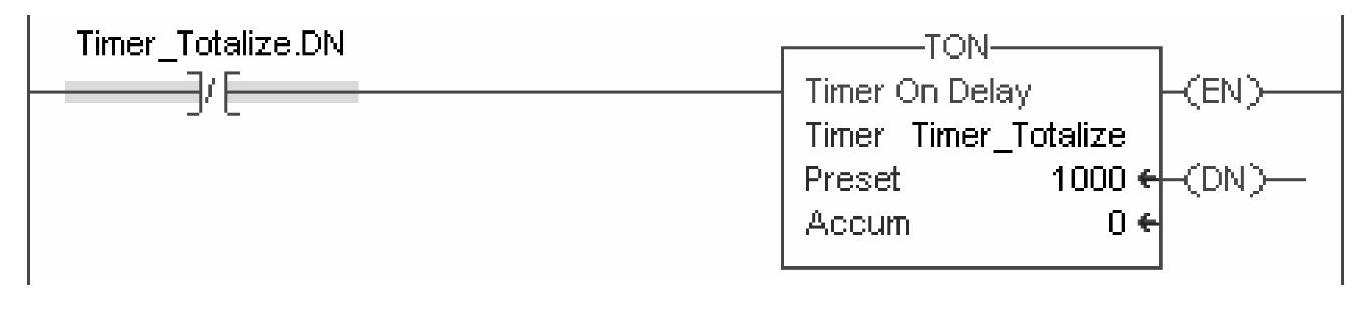
图6-7 计时器每秒钟产生一个动作脉冲

下面要解决的是如何积累数据，用一条ADD指令，每秒钟对采集的数据相加一次，然后送回作为累加器的存储单元，因为我们明了这个自复位计时器的DN位置位能够且只能够存在一个扫描周期，所以很放心ADD指令1s只能相加一次，不会更多，如图6-8所示。

现在比较纠结的问题出现了，如何将流量转为容量呢？大家应该没有忘记，这个数据是一个吨/小时的信号采集来的，而数据又在按每秒积累。这时大家不约而同地想到了那个数字3600，这是小时和秒的换算。你可能会说，这很简单，把采集积累的数据除以3600，得到的容量单位就是吨，开始我也这么想来着。

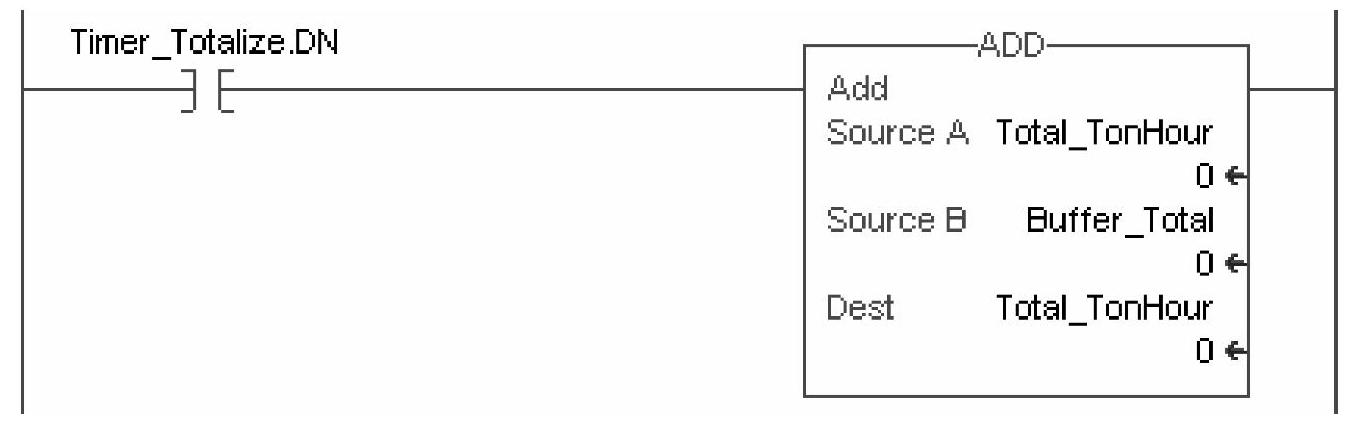
图6-8 每秒一次的流量累加

下载到控制器的程序一运行就报错溢出了！解释一下，当时我用的是PLC5，那是16位寄存器的内存单元，可以想想，16位的最大数据存储是32767，千位数的采集积累十几秒后就溢出了。当然Logix控制器提升到了32位的存储容量，可容纳的数据范围达到了2147483647，存放一天的产量累积绰绰有余，不会发生溢出。如果我想要更高的精度，Logix控制器的模拟量模块早就不是千位数的精度了，如果定标在万位数，这个容量就可能不够存放一天了，更何况存储的未必是一天的累积量，即使是Logix控制器32位的数据容量，依然面临不够存放的困境。其实我们一直在纠结数据单元的容量够不够，就是因为我们一直想用除法解决这个换算的问题。不妨换个思路试一下。

于是我编写了这样的梯级逻辑来解决换算的问题，如图6-9所示。其实除法的本质就是累减法，完全可以用减法来代替除法。

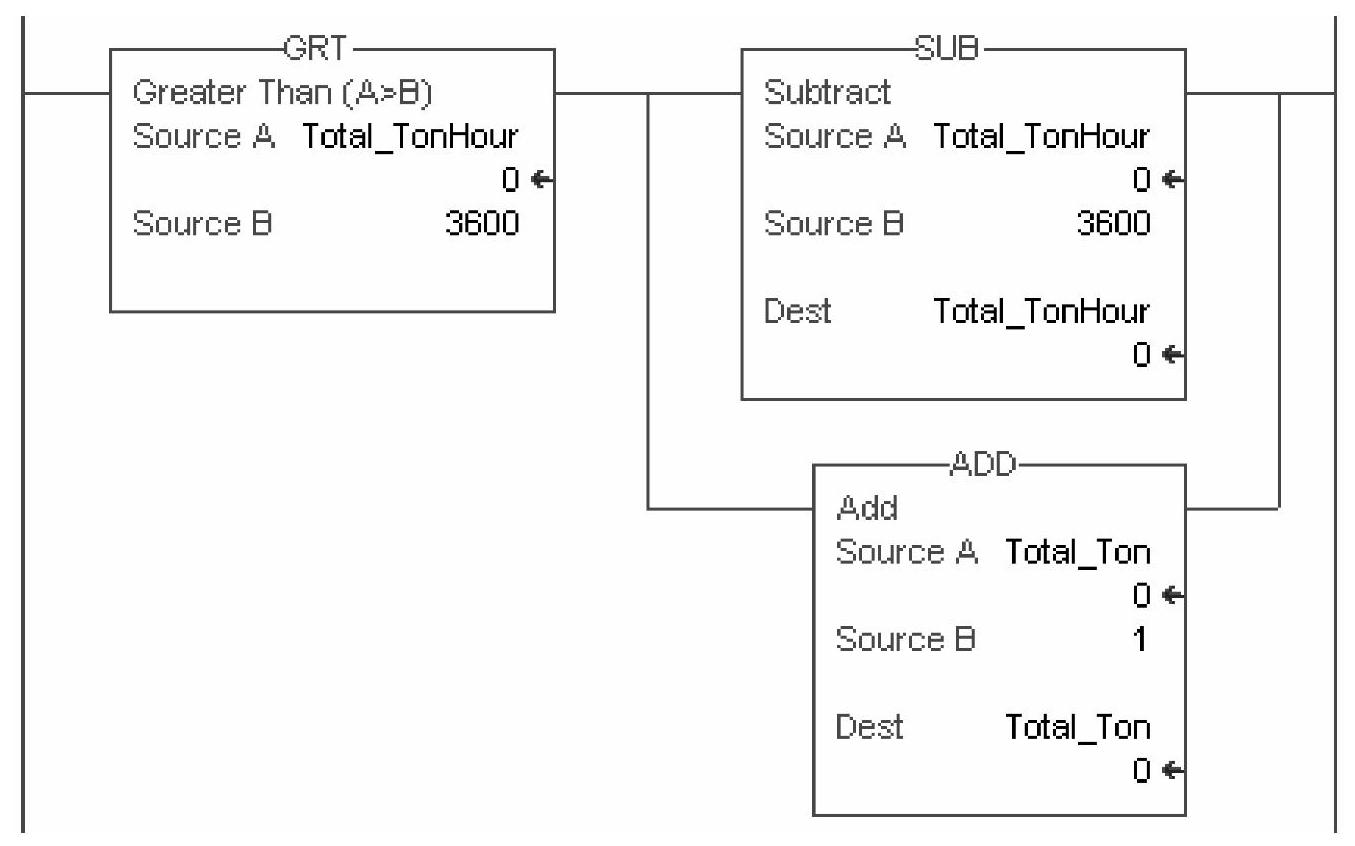
图6-9 累减法代替除法

用一条比较指令来决定这个操作，当累积量大于3600时，就从累积量中减去3600，同时在设定的以吨为单位的累积器中加1，这样我们永远也不要担心累积量是否会溢出。我们得到结果是相当准确的，除了有不到一吨的延时残存，那是累积不到3600的那一部分余值。

在一个高速运算的系统中，乘除法未必优于加减法！何况计算机中的乘除法就是加减法的累积，即使我们使用了除法指令，计算机也会换成减法来运算，我们不过是回到最基础的处理模式罢了。

现在我们来讨论另外一个问题，究竟是先把流量换成吨再累积，还是先累积再换成吨呢？如果我们采用了除法现将流量换算成吨的容量，然后再进行累积，就不可避免的会有累积误差；如果先累积，再换算成我们想得到的容量，我们又会担心累积容量溢出的问题。如采用累减法解决问题，两种忧虑都没有了。(www.xing528.com)

我们将编程设备的模拟量通道1的模拟数据当做流量采集，编写如图6-10所示的梯级逻辑，乘法指令直接使用了定标比例系数SC.K，请注意梯级的顺序，并运行测试通过。

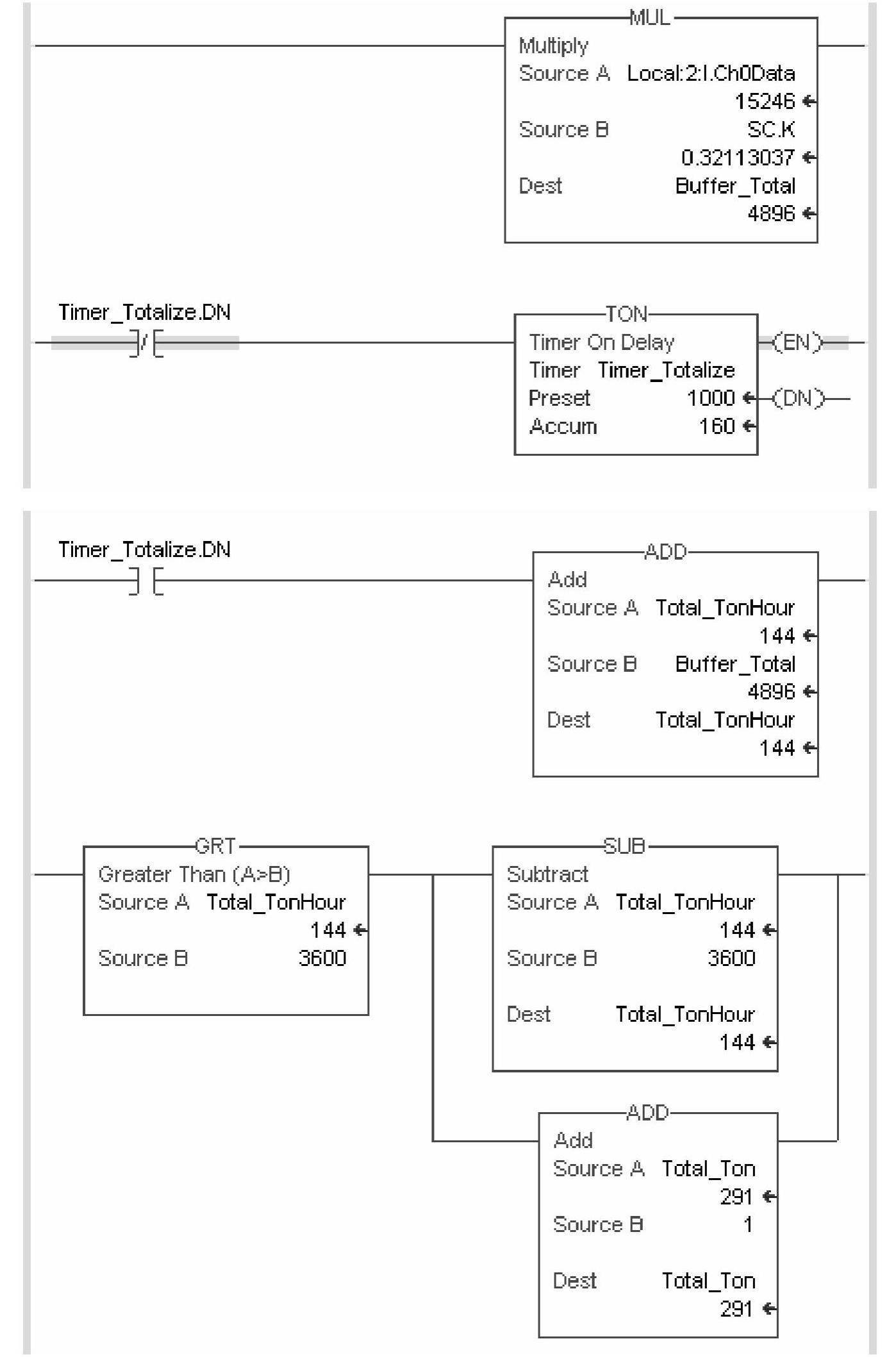
图6-10 处理流量累积的梯级逻辑

这里我们延伸讨论一下关于数据处理环节的问题。我们知道，整个系统的信息流动，在不同的处理环节，是不同的载体、不同的表达形式和不同的数据范围。例如一个温度被采集到人机界面显示，所经历的信息环节变换过程是：

物理量温度（范围-40～+60）→物理电信号模拟量4～20mA→数据0～31140→定标数据0～10000→换算-40～+60→人机界面显示。

为什么在模拟量定标时不直接定为-40～+60呢？这样做无疑影响了A/D转换的精度。所以我们宁愿对模拟量模块定标较大的数据范围，以获得更好的A/D换算精度，然后再换算到温度范围。在控制器中的每一个数据处理环节，我们考虑的是怎样获得更高的精度和最少的积累误差，而不是急于还原数据的原来面目。在使用算术指令时最需要顾虑的，不仅仅是如何获得运算的正确结果，还需考虑如何避免精度的损失。

上面所讨论的问题，还有一个地方有遗漏，实际上我们得到的数据单位并不是吨，因为从吨/小时传感器的电压或电流信号到模/数转换后的数据，还有一个换算关系需要核准，我们将最后得到的数据乘上这个核准的系数，才是真正的单位吨。我们先考虑数据处理中确保精度的最佳方案，最后再考虑换算关系。在数据信息的传递过程中，未必每个环节都是数据的真实面目。所以，不要急于将数据换算成真实的面目。

我们再来看一个例子，前面第5章中，有一个关于发动机运行时间累计的例子，其累计值将为机组保养提供依据，这个时间的累计值是需要作后续的数据处理的，因为需求是当发动机运行若干时间后，要给出保养的提示信息，这个时间要求以小时为单位，并以此判定。我们先假定发动机运行3000h后，要求触发提示信息，梯级逻辑编写如图6-11所示。

比较指令对发动机运转速度值进行判断并决定梯级条件，当速度达到并超过额定值时，认定发动机处在正常运转状态，比较结果令梯级条件成立，保持型计时器开始计时；当发动机运转速度低于比较值时，梯级条件不成立，保持型计时器停止计时累积，并且累加值保持不变。如此重复，计时器的累加值可能是断断续续记录了时间的积累，由于计时基值是毫秒，所以这是毫秒为单位的时间积累。

类似前面自来水流量的累积做法，为了避免累积误差，宜采用累减法来解决，每当计时器的累加值大于3600000ms，也即1h的时间，便从计时器累加值中减去3600000，同时给运行时间累积值RunTimeTotalize增加1，以累积小时单位的累积器随时提供了发动机运转的累积时间以供参考。可以看出来，累积器的时间单位是可以调整的，取决于你希望用怎样的单位去积累时间，改变比较值和相减的量便改变了时间的单位。此处比较值和减去的数值都是3600000，所以运行时间累加器所表达的数值是小时，即积累时间标签RunTimeTotalize的单位是小时。

当发动机保养完毕，即将开始新一轮的时间累积，可以将计时器累加值和小时累积值清零，并将提示信息复位，以便下次重新开始，梯级逻辑编写如图6-12所示。正如所有实际例程所做的那样，附加于算术运算指令信息处理的梯级逻辑也是必不可少的。

一段完整的数据采集、数据处理和复位操作的梯级逻辑，如图6-13所示，并运行测试通过。

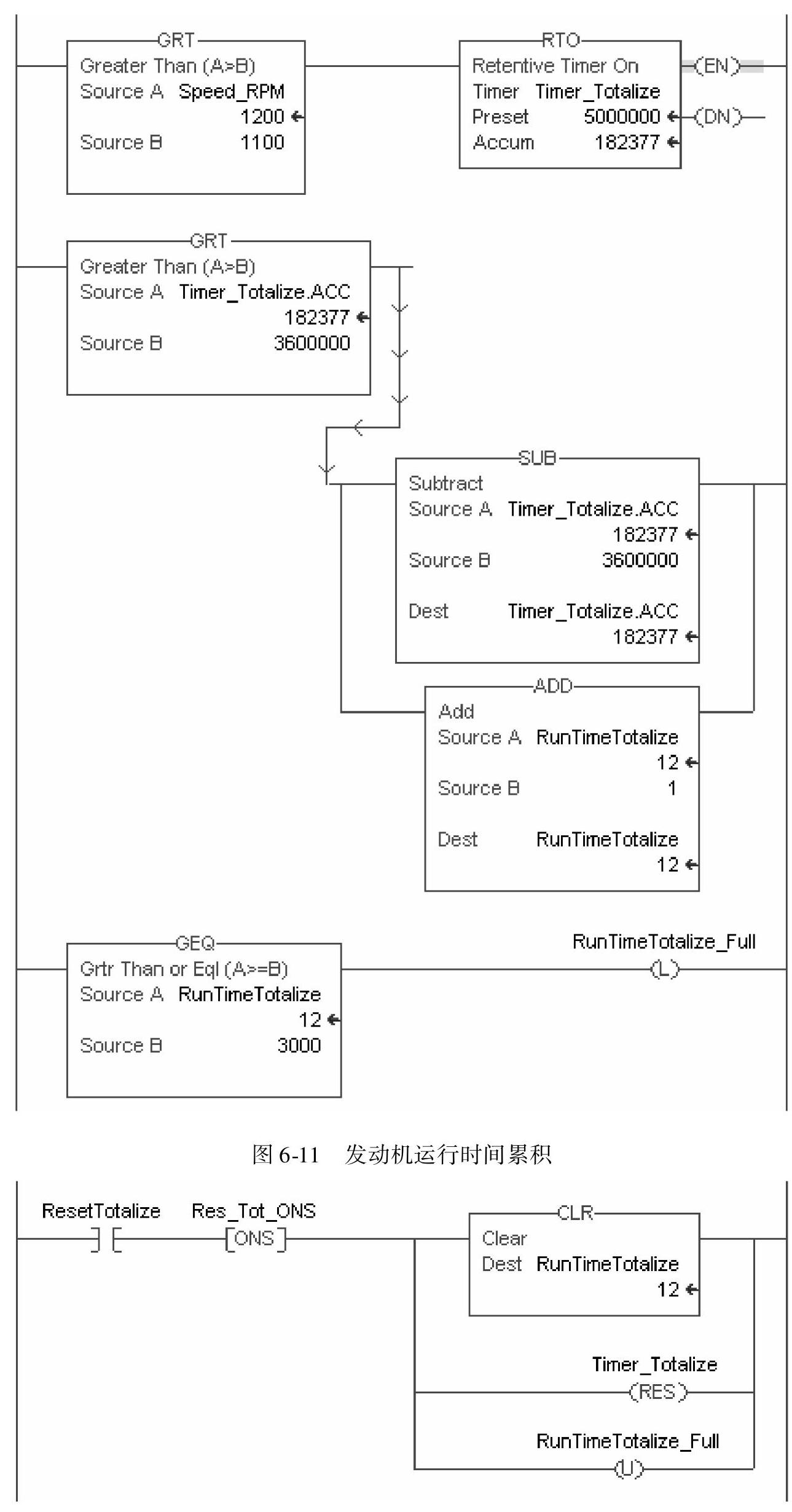
图6-12 复位所有数据和状态

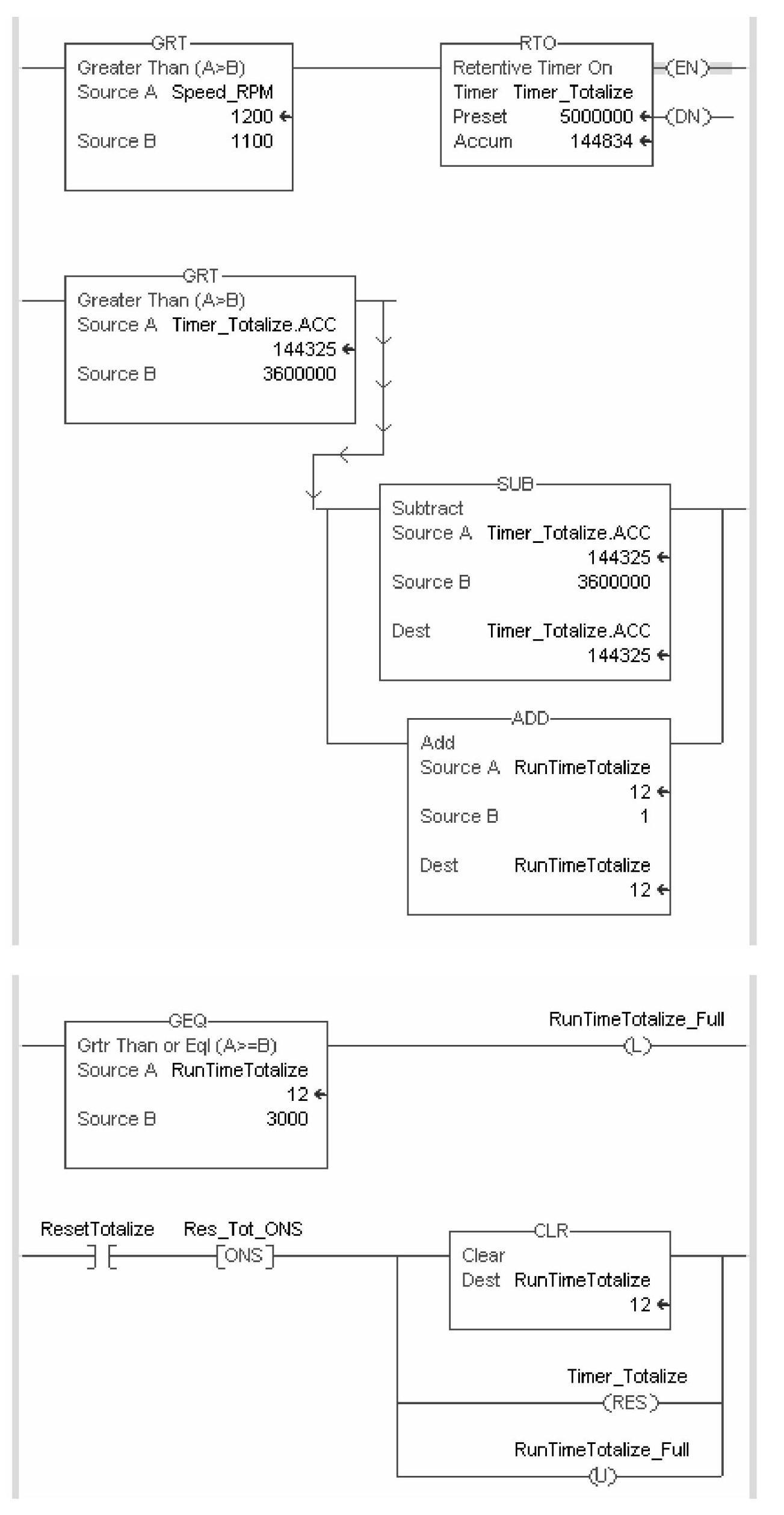
图6-13 发动机运行时间积累完整的梯级逻辑