基于水功能区的纳污能力计算方法及应用成果

1.二维水质模型解析解

(1)顺直均匀河流二维水质模型解析解。顺直均匀河流的水质基本方程详见式(4.28)。在顺直均匀河流中,对微分方程进行求解时,需考虑排污口的位置、污染源排放形式及河流的规模。例如,一些规模较小的河流,污染物扩散到岸边后会出现岸线对污染物的吸收、反射现象,从不利角度考虑,一般取岸线的完全反射。也有一些情况是河面无限宽,污染物扩散不受岸线限制。本小节将按照无岸线限制和有岸线限制两种情况,给出式(4.34)的解析解。

1)无岸线限制。根据前文所述,在横向混合区,河面无限,以排污口所在位置为原点,污染物连续稳定排放,污染物进入水体后垂向均匀混合,对于均匀河段,流速u在横向上均匀分布,因此,x轴两侧的浓度是对称分布的。天岸边限制的点源污染扩散示意图见图4.9。

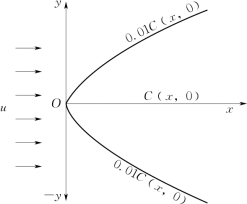
图4.9　无岸线限制的点源污染扩散示意图

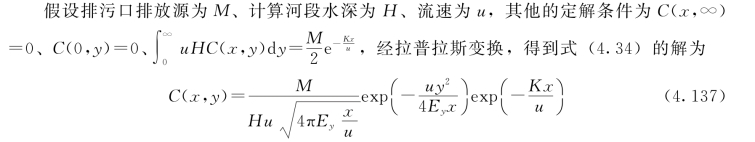
其他符号意义同前。

2)有岸线限制。

a.单边反射。如图4.10所示,在距离河流右岸b′处,设有一处稳定的污染源M(真源),污染物进入河流后,在向下游迁移扩散过程中同时向两边扩散。当右侧污染物扩散(图4.10中曲线123)遭遇岸边被全部反射后,分布为虚线23′,以岸边为界面将实线23向河中反褶。虚线23′用镜中映射的概念计算,即在岸边右侧y=2b′处设置一个与真源相同的像源,像源在无边界限制下在x断面处形成的污染浓度分布为C(x,2b′-y)。

经岸边反射后,真源在河岸左侧水域形成的污染浓度分布C(x,y)就等于真源和像源在河岸左侧水域分别形成的浓度分布叠加,浓度叠加结果用数学公式可描述为

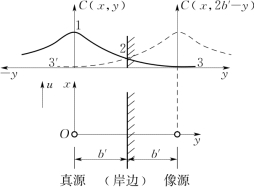
图4.10　单边反射的点源污染扩散示意图

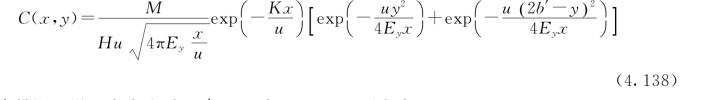
当排污口设置在岸边时,b′=0,式(4.138)可变为

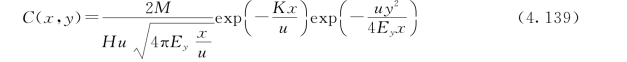
b.双边反射。设计算水域河宽为B,排放口位于河道中心,按照单边反射的原理,此时的污染源分布应该是真源与两边的像源经多次反射后叠加而来。双边反射的点源污染扩散示意图见图4.11。

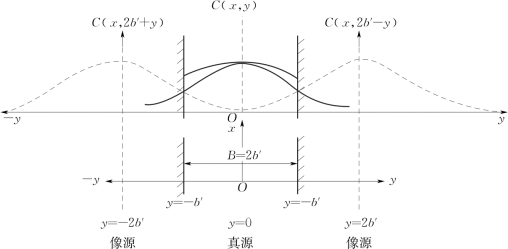
图4.11　双边反射的点源污染扩散示意图

每一个岸边第一次反射的污染物浓度到达对岸后又产生反射,这样周而复始。因此,河道两侧岸边均有污水的像源点,它们到河道中心的距离依次为±2b′、±4b′、±6b′、…、±2nb′。将真源与像源的浓度分布叠加,可用数学表达式表述为

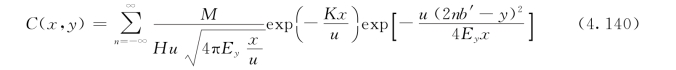
式中 n——反射次数;

其他符号意义同前。

一般情况下,只需要考虑1～2次反射。考虑双边一次反射的解为(www.xing528.com)

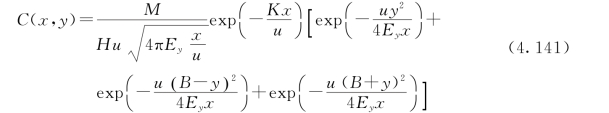
当排污口设置在岸边时,式(4.141)可变为

1)岸边排放,有

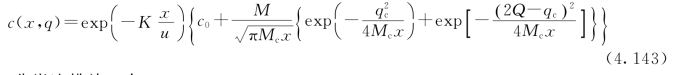
2)非岸边排放,有

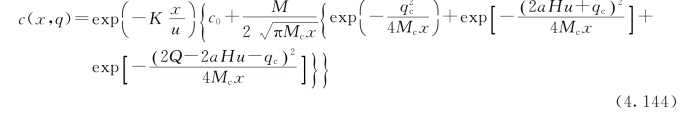
式中 a——排放口距岸边距离,m;

其他符号意义同前。

2.模型适用要求

(1)顺直均匀河段二维水质模型。模型适用于稳态条件下的顺直、均匀河段混合过程段;模型忽略了纵向离散作用,仅考虑横向扩散作用;对于非持久性污染物,还需考虑污染物的衰减作用。

(2)累积流量坐标下的二维水质模型。适用于弯曲河段混合过程段。其他要求同顺直均匀河段。

3.纳污能力计算模型

(1)顺直均匀河段纳污能力计算模型。对于一个划定的水功能区而言,假设水功能区长度为L,河段上断面非持久性计算因子初始浓度为C0,污染物岸边排放,排放处距上断面距离为x,以岸边污染物浓度作为下游控制断面的浓度时,即y=0,考虑岸边一次反射,参照式(4.139),此时的排污口下游任一点污染物浓度数学表达式为

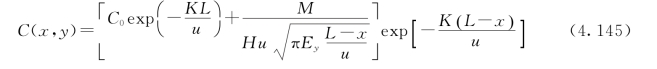
据此反推纳污能力计算公式,得

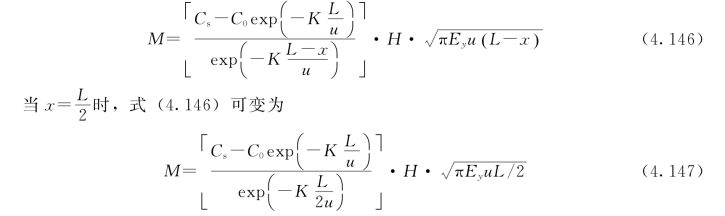
其他符号意义同前。

据此反推纳污能力计算公式为

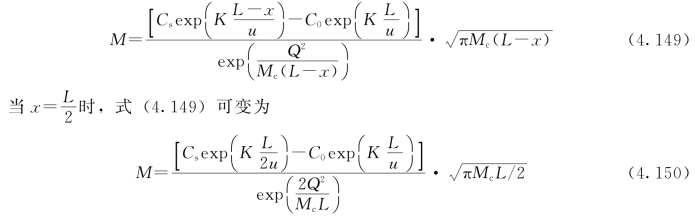
其他符号意义同前。