高中生对直线与圆锥曲线问题理解水平调查结果

在某中学高三的理科班的重点班中随机抽取一个，平行班中随机抽取一个。一个重点班和一个平行班，在一定程度上形成对照，可以调查高中生尤其是高三学生对于直线与圆锥曲线问题理解水平的发展状况。共发放问卷105份，全部收回。样本中，重点班60人，平行班45人。

研究采用了质性与量化的研究方法。质性的研究方法是结合文献以及对于直线与圆锥曲线问题的问题解决进行理性分析，量化的研究方法是在质性分析的基础上自编测试题目探寻学生在处理直线与圆锥曲线问题时呈现出的差异性和关联性，核心是编制测试题，难点是测试成绩的确定。对此，运用SOLO分类评价法作为研究工具来测试学生对知识掌握的水平。SOLO是观察到的学习成果的结构，将学习效果分为五个层次：①前结构水平。学生并没有理解学习文本，找不到任何解决问题的办法，记为0水平。②单一结构水平。关注题目中的相应材料，可以找到一个解决问题的途径，记为1水平。③多元结构水平。学生找到构成问题与越来越多的正确的相关特征，但只是简单罗列这些要点，还没有形成将它们进行有机整合的能力，记为2水平。④关联结构水平。学生会整合各部分的内容，使其成为一个有机的整体，体现在能回答或解决较为复杂的具体问题，记为3水平。⑤拓展抽象水平。学生会归整问题来学习更多的抽象文本，代表一种更高水平的学习能力，这一水平表现出更强的钻研和创造能力，记为4水平。

（一）水平的划分和测试问卷设计

北师大版的必修2第二章为解析几何初步知识，包括直线与圆。选修教材2-1中第三章为圆锥曲线，包括椭圆、双曲线、抛物线、曲线和方程。依据SOLO分类评价标准，划分出高中生关于圆锥曲线理解水平的层次。在圆锥曲线的定义和性质中，0水平表示不能叙述圆锥曲线的定义，不能识别出圆锥曲线的内容，找不到解决办法，即对知识很是盲目，几乎白纸一张。1水平表示能够叙述圆锥曲线的定义，但却不能根据定义求出曲线的方程，更进一步的认识不具备，没有形成思路。2水平表示知道圆锥曲线的定义，对其中满足的条件比较熟悉，能求出圆锥曲线方程，对圆锥曲线方程与性质的联系有初步的了解。3水平表示能理解圆锥曲线的定义，熟练求出圆锥曲线的方程，能够熟练理解圆锥曲线的常见性质。4水平表示理解圆锥曲线的定义和其区别与联系，对圆锥曲线的统一定义有一定的认识，能够结合图形将圆锥曲线的方程和性质结合在一起，甚至能够以圆锥曲线的定义和性质为基础，研究圆锥曲线的进一步性质。

在直线与圆锥曲线的综合问题里，0水平代表对直线和圆锥曲线的关系连最基本的联立方程的思想都没有，更毋言缺乏求解的方向。1水平表示对于直线和圆锥曲线的关系有初步的认识，能够对直线的方程熟悉，会联立方程，但对其中的简单问题却不能求解。2水平表示能联立直线与圆锥曲线的方程，可以求解比较简单的综合性问题。3水平代表可以熟练地解决综合性问题，对于常见的题目类型很熟练，比较顺利地求解。4水平表示能够综合图形，分类讨论，比较完善解答直线与圆锥曲线方面的综合性问题，对于一些特殊的问题的转化能够用一定的特殊技巧熟练地完成。

根据上述划分设计了测试题目，共7道测试题，题目难度由低到高依次呈现，每道题根据作答情况确定学生掌握的水平层次。测试时间为60分钟，考查高中生尤其是高三学生对于圆锥曲线的定义、简单性质以及直线与圆锥曲线综合性问题的掌握程度。第一步是测试卷的编制、修订、测试和完善的过程，依据对学习者掌握水平的界定随机选取一个班级进行预测试，根据测试的结果对问卷进行修改和完善。第二步是对所选择的样本实施测试和判定水平的层次。第三步是进行数据的整理和分析。将学生的测试水平按照不同的变量输入Excel，采用描述统计对样本和总体进行统计分析，采用T检验对各个变量和直线与圆锥曲线问题的求解之间的差异的显著性进行分析。

（二）数据整理与分析

我们知道，圆锥曲线的定义和性质是直线与圆锥曲线综合问题的基础，指明了综合性问题求解的方向。下面就对调查的结果按照不同的要求进行统计分析。

表14-1　学生在圆锥曲线的定义和性质维度上测试水平的分布情况

表14-1表明，在圆锥曲线的定义和性质这一维度上，在2水平和3水平的学生比较多，分别占总人数的35.20%和24.80%。这说明很多学生对于圆锥曲线的定义比较熟悉，能够根据定义求出圆锥曲线的方程，对圆锥曲线简单性质也能求出。1水平的学生比较少，说明大部分学生对定义比较清楚，但是求解其简单的性质还存在问题，对于圆锥曲线所呈现的性质不能求解，也就是将定义和性质不能结合起来，形成知识之间的脱节，这个利用定义进行简单应用的跨越没有完成。0水平和4水平的学生相差不大，说明学生的两极分化现象比较严重，掌握精通的学生有且不少，对于过两点的椭圆方程的求解都很熟练，能够利用椭圆方程的一般式这样的技巧方便地求解，但同时对圆锥曲线定义这样的基本概念都没有的学生还有很多，教学中不容小觑。

表14-2　学生在综合应用维度上测试水平的统计

表14-2表明，在直线与圆锥曲线的综合应用这一维度上，在0水平和1水平的学生很多，分别占总人数的32.40%和23.80%，占到六成多，说明很多学生对于直线与圆锥曲线的综合应用水平特别薄弱，很多学生在设直线的方程时都没有注意到其形式的局限性，导致解的遗漏、不完善。2水平达到20.00%，能够对直线与圆锥曲线中常见的简单问题进行求解，但其中或多或少存在一些瑕疵和不完美的地方。3水平达到15.20%，可以对比较常见的直线与圆锥曲线的综合性问题熟练地求解，在解答的过程中对于问题的认识还比较深刻。达到4水平的仅为8.60%，对难度较大的、转化比较麻烦的直线与圆锥曲线的综合性问题处理的人数很少，且主要积聚在重点班。总之，可以看到，学生在直线与圆锥曲线的综合性问题上普遍能力不足，不能深刻认识，达不到灵活运用的程度，对于数形结合的思想和分类讨论的思想不能认真分析，熟练掌握。同时，注意到，很多学生在联立直线与圆锥曲线的方程进行消元的过程中折戟沉沙，得不到正确的表达式。(www.xing528.com)

表14-3　平行班学生与测试水平的分布情况

表14-3表明，平行班的学生不论是在定义或者性质还是综合性问题上所呈现的主要在0水平，学生对圆锥曲线的基本概念不了解，直线里面的基本知识缺乏，表示直线都有很明显的错误，基础很不牢固。在1水平却有部分学生能够解答，即求椭圆的标准方程和离心率的计算方面以及联立直线和圆锥曲线的思想有一定的体现。这说明尽管很多学生对概念方面的知识不熟练，但依然有部分学生能够较好地完成基础题目的解答。同时，注意到，在完成1水平的学生中，在0水平的问题上也有认识错误的。这说明，概念是基础，一些学生不注重基础知识的积累，但是常见的基础题目却能够解答出来，这在平行班级经常见到，但是基础不牢，没有厚积薄发的实力，导致后劲不足，整体水平也一般，不会特别突出。在3水平和4水平的人数很少，堪称平行班的学霸，但是综合性问题中的4水平没有学生完成。

表14-4　重点班学生与测试水平的统计

表14-4表明，重点班的学生在定义或者性质的掌握上所呈现的主要在2水平和3水平，也就是学生对圆锥曲线的基本概念比较了解，对于曲线离心率的解答比较顺利，但还没有达到熟练的程度。尽管0水平没有学生，但可以看到学生的基础并不怎么好。在综合性问题的解答中，各个水平都有分布，相对比较均匀，说明学生在各个掌握层次的都有，整体效果一般，但联立直线和圆锥曲线的思想能够体现，有些甚至有特色。但也应该注意到还有16.7%的学生对于综合性问题的求解差距较大，落后了。

表14-5　显著性检验

注：取α=0.05。

在分析平行班和重点班对问题的理解差异时，对重点班和平行班在曲线的定义和性质与综合性问题方面进行T检验。从表14-5可以看出，重点班学生在圆锥曲线的概念和定义方面与平行班的情况差异明显，而在综合性问题上尽管差异也很明显，但是参数较小。这说明尽管重点班学生的基础较平行班好，但是在综合性问题上还没有形成整体的思维。

表14-6　对圆锥曲线问题难度、认识的统计

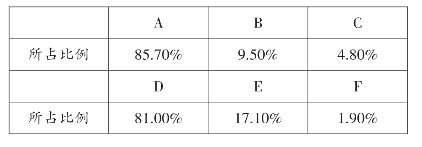
以上分析表明，平行班的学生在圆锥曲线的知识掌握方面均处于较低水平，对所学的知识没有深入认识，即使有很多基础知识也没有牢固掌握，而重点班学生的掌握水平尽管普遍高于平行班，但是水平依然不高，对难点问题没有熟练掌握，对问题的认识肤浅，缺乏深度，给学生留下深刻的印象后容易形成“一朝被蛇咬，十年怕井绳”的恐惧。直线与圆锥曲线的综合性问题难度大，才会出现表14-6的结果。见了这样的问题，产生恐惧心理，甚至形成恶性循环，难度大，败下阵来，逐步地放弃问题的解决。