例7:某超市计划按月订购一种酸奶,每天的进货量相同,进货成本每瓶4元,售价每瓶6元,未出售的酸奶降价处理,以每瓶2元的价格当天全部处理完,根据往年销售经验,每天需求量与当天最高气温有关。如果最高气温不低于25摄氏度,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20摄氏度,需求量为200瓶。为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得出下面的频数分布表11-1。
表11-1 气温与天数的频数分布表

以最高气温位于各区间的频率代表最高气温位于该区间的概率。
(1)求六月份酸奶一天的需求量x(单位:瓶)的分布列。
(2)设六月份一天销售这样的酸奶的利润为y(单位:元),当六月份酸奶一天的进货量n(单位:瓶)为多少时,y的数学期望达到最大值?
教学目标:理解题目中蕴含的数量关系,能够将实际问题抽象概括成数学问题,找到对应的数学模型并建立数学模型,培养学生的建模能力和抽象概括能力,在解决实际问题的过程中,培养学生数学应用意识,体会数学在社会和生活中的重要作用。
教学策略:重视学生的阅读理解能力,要让学生能够独立地分析问题,培养学生将实际问题抽象概括成数学问题的能力,这样也培养了学生良好的自学习惯,学生会比较容易地想到建立概率模型,提高了学生的模型意识,然后引导学生利用概率知识解决实际问题,进一步加强数学与生活的联系,培养数学应用意识。
教学内容:
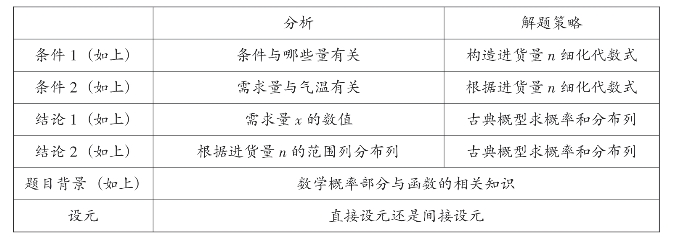
阅读题目找关系:让学生自主理解题目信息,找出条件和结论,并填好表11-2(尽量小组合作或者独立思考完成)。
条件1:进货成本每瓶4元,售价每瓶6元,未出售的酸奶降价处理,以每瓶2元的价格当天全部处理完。
条件2:如果最高气温不低于25摄氏度,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20摄氏度,需求量为200瓶。
结论1:求六月份酸奶一天的需求量x(单位:瓶)的分布列。
结论2:设六月份一天销售这样的酸奶的利润为y(单位:元),当六月份酸奶一天的进货量n(单位:瓶)为多少时,y的数学期望达到最大值?
表11-2 条件和结论
 (https://www.xing528.com)
(https://www.xing528.com)
建立数学模型:要将以上两个问题的条件和结论加以归纳分析,将现实的实际问题抽象成数学模型,建立数学与生活的关联,运用相关数学知识手段在一系列的探究中解决问题,这是观察、思考、分析的过程。
(1)利润=(6-4)n-亏损。
(2)细化为y=n(6-4)=2n(n≤200),y=200×2+(n-200)(-2)=800-2n(200﹤n≤300),y=300×2+(n-300)(-2)=1200-2n(300﹤n≤500)。
其中,进货量n的范围是200﹤n≤500。
进货量n的概率分布表如表11-3所示。
表11-3 进货量n的概率分布表

代数求解:
(1)需求量x的取值分别为200,300,500时,需求量x分别对应的概率为![]()
关于进货量n的分布列如表11-4所示。
表11-4 关于进货量n的分布列

(2)根据数学期望公式,当200﹤n≤300时,E(y)=160+1.2n,当300﹤n≤500时,E(y)=640-0.4n。
结果还原:将运算结果还原为实际问题,检验得出应用问题答案结论,即当n=300时,E(y)=160+1.2n=520,即当六月份酸奶一天的进货量n为300时,y的数学期望达到最大值520。
教学总结:数学创新型应用题主要体现了数学建模这一核心素养,要重视数学实际问题与生活、生产的联系,培养学生建立正确数学模型的能力。在解决应用题的过程中,要先分析材料,将有效数学信息抽象提取出来,再根据知识的背景进行代数运算,主要体现了数学抽象、数学运算和数学建模的数学核心素养。正确进行数学应用题的教学,注重核心素养的培养,对学生解题能力、思维能力和创新能力都有很大提高。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




