例5:在信息化时代,电脑技术和数学联系紧密,计算机想要实现对信息的处理,就要将其转化为二进制数。其中,二进制数的基本规律就是“逢二进一”。比如,二进制[1101]2可用十进制数将其表示为1×23+1×22+0×21+1×20=13。根据这一规律,二进制数[111…11]2利用十进制数可表示为( )。
A.2n+1-1 B.2n+1-2 C.2n-1 D.2n+2-4
教学目标:理解二进制与十进制互化的基本规律,能够运用类比的方法,用十进制数表示二进制数[111…11]2,能发现十进制与二进制转化的实质是等比数列求和公式,并熟练运用公式求解问题,让学生体会到这是数列模型的应用,培养学生数学建模意识,让学生体会数学与信息科技的密切联系,提高数学应用意识。
教学策略:根据信息给予题的特点,教师首先要将阅读题目的权利交给学生,由学生自行理解并抽象概括出关键信息,培养学生抽象概括能力,然后引导学生观察、发现规律,找出数学模型,培养建模意识,最后由学生运用数列求和公式解决问题。通过熟练运用公式,培养学生运算能力。因此,可以看出本题的设置主要培养学生的数学抽象素养、数学模型素养、数学运算素养。
解:[111…11]2=1×2n+1×2n-1+…+1×21+1×20=2n-1。
分析:这是一道新定义性质型创新题。在信息化时代,计算机的发展与数学紧密相连,让学生了解数学与科技的联系,在题目中引入二进制,简要介绍了二进制与十进制之间的内在联系和本质,以考查学生分析、观察、研究题目信息及内隐信息的综合能力。将十进制的表示方法与数列求和公式联系起来,根据[1101]2的展开方法,通过类比运用等比数列求和公式解出[111…11]2的结果。这类题重在引导学生运用类比思想,把握新定义性质的数学对象的本质特征,挖掘其与已学知识(等比数列求和公式)的有效联系,掌握关键点。在学生已经充分阅读理解题目信息的基础上,教师要引导学生对新性质进行抽象概括,在学生头脑中建立数学内容的本体结构,然后灵活地运用,在头脑中找到已经建构的相关知识内容解决问题,主要培养了学生类比思想、数学抽象素养、数学建模素养、数学运算素养。
例6:定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都是同一个常数,那么这个数列就叫作等和数列,这个常数叫作该数列的公和。已知数列{an}是等和数列,且a1=2,公和为5,那么al8=( ),该数列的前n项和Sn的计算公式为( )。
教学目标:理解“等和数列”的本质属性,会运用等和数列性质进行运算,能够类比等差数列求和公式的推导过程求出等和数列前n项和公式。
教学策略:根据新定义的等和数列的概念,引导学生回忆等差数列概念,建立起新旧知识的联系,类比等差数列性质,猜想、归纳等和数列的性质,再类比等差数列求和公式的推导过程,推导出等和数列的前n项和公式。(https://www.xing528.com)
解:以“等和数列”为载体,关键是要运用等差数列的有关知识及获得这些知识的数学活动经验,通过类比等差数列性质和运算,归纳类比得出等和数列概念和性质。
由等和数列性质,有an+an+1=d,an+1+an+2=d(概念类比),
两式相减(方法类比)得an+2-an=0,即an+2=an,公和是5,则a2=3,因此a2n-1=2,a2n=3(n=1,2,3,…),所以得到a18=3。
当n为偶数时,![]()
当n为奇数时,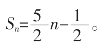
分析:这是一道类比等差数列的概念定义等和数列的创新题,属于定义新运算型创新题。本题源自高考题,考查了运用类比思想解决数列创新题的能力。类比推理就是根据两个或者两类数学对象在某些属性上相同,推断出它们在另外的属性上(这一属性在类比对象那里已然具有,而要进行类比的对象尚不具有的属性)也相同的一种推理。在本题中,以等差数列为类比对象,由前面学过等差数列的相关的运算、解题方法、性质等特征,通过观察、类比、分析寻找规律,结合相关的数学方法、数学思想和数列的基础知识,重点考查学生探究、推理、创造的能力,同时要求学生在较短的时间内理解题目含义,独立解决问题,学生要有较强的心理素质和独立获取知识的能力。
教学总结:通过以上两个定义信息型创新题的实例分析,我们发现这类创新题着重考查学生对归纳、类比推理思想的掌握。类比的方法很多,主要有概念、运算、性质、方法和结构,教师可以直接讲授采用哪种方法,也可以以提问的形式引导学生思考、探究、总结,学生的思维活动先经历了对概念的理解,后来是经历方法类比的过程,最后升华到经历对类比式结构的深入理解的过程。教师要引导学生理解类比思想对于定义型创新题的重要作用,此类题目的训练可以提高学生类比推理的思维能力,进一步培养逻辑推理素养。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




