教材九年级上册第六章第二节介绍了反比例函数的图像和性质。在此之前，学生已经学习了反比例函数的概念，为本节课的学习打下了一定的基础。其实，“图形”和“性质”本身就是“形”和“数”。通过分析图像，我们可以确定函数的性质。通过分析解析式，我们可以确定函数的大致走向。由“数”忆“形”，由“形”思“数”，处处体现了数形结合的思想方法。
（一）教学片段
片段1：
核心问题：反比例函数
与
的图像有什么共同特征以及不同点？
教师在PPT中直接展示引导式四个问题：
（1）在形状和位置上有什么相同点和不同点？
（2）在每个象限内，这两个图像是如何变化的？
（3）这两个函数的图像与坐标轴有什么位置关系呢？
（4）这些不同点和相同点是由什么决定的呢？
学生认真思考。
教师（问题①）：首先，大家看一下，这两个函数的图像在形状和位置上有什么相同点和不同点？
学生1：相同点是这两个函数的图像都是由两条曲线构成，不同点是
图像在一、三象限，
的图像在二、四象限。
教师（问题②）：嗯，那也就是说这两个图像都是双曲线，那在每个象限内，这两个图像是如何变化的？
学生2：在每个象限内，
的图像从左到右依次下降
，的图像从左到右依次上升。
教师（问题③）：非常好。那大家再想一想，这两个函数的图像与坐标轴有什么位置关系呢？
学生3：随着x值的不断增大或减小，曲线越来越接近坐标轴。
教师（问题④）：这些不同点和相同点是由什么决定的呢？
学生（齐答）：k的符号。(www.xing528.com)
片段2：
教师：观察反比例函数
的图像（如图9-3所示），思考下面问题。
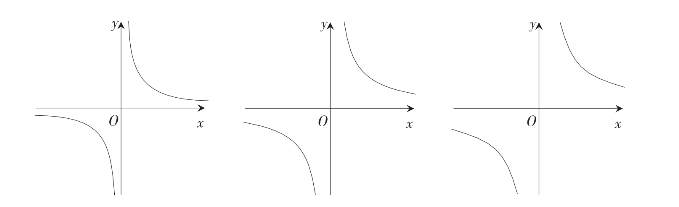
图9-3 图像
教师（问题1）：这三个图像的形状是什么？
学生：图像的形状都是双曲线。
教师（问题2）：好，都是双曲线。那图像位于哪几个象限？
学生：图像都位于第一、三象限。
教师（问题3）：在每一象限内，y随x的变化如何变化？
学生：在每一象限内，y随x的增大而减小。
教师：恩，非常好，这个条件也说得很清楚，在每一象限内。
接着，引导学生总结k﹥0时反比例函数的增减性质……
（二）案例评析
本案例中两个片段均选自实习期间李教师的课堂实录，片段1是第一课时中指导学生画出反比例函数
与
的图像后，引导其探索性质的小片段，片段2是第二课时中在画出三个k﹥0的反比例函数图像后探索其增减性质的小片段。接下来，将就问题串在数形结合思想方法教学中存在的问题进行点评。
片段1中，教师只是单纯地让学生掌握了反比例函数的性质，而弱化了数学思考方面教学目标的掌握。其具体体现在，为了帮助学生找到两个反比例函数图像的相同点和不同点，教师没有给学生自主总结图像特征的机会，就直接在课件中展示问题串，并依次提问引导。这样做，看似是帮助学生观察和理解图像，实则阻碍了学生的思考能力，阻碍了对数形结合思想方法的渗透。由于学生之前已经学习过一次函数的图像和性质，具备了一定的处理相关问题的经验，所以教师在提问时，应该更多地给予学生思考空间，注重思维发展过程。教师应让学生仔细思考、小组交流，相信学生能够得出相关的性质。教师此时适时引导，再予以补充，加深印象，能够更好地帮助学生理解“数”“形”之间的转化。
片段2中教师的问题设置缺乏“数”到“形”的渗透。反比例函数的图像和性质一课，本身就体现了“形”和“数”之间的转换。讲述性质的过程，也是更好地向学生渗透“形”到“数”转变的过程。片段2在总结k﹥0时反比例函数的性质时，是通过引导学生对图像进行观察得出结论的。其实，在通过图像总结性质的过程中，正是“形”向“数”渗透的好时机。此时，如果李教师能更深入地分析，引导学生从解析式的角度分析问题2和问题3，将会让学生对“数”和“形”的理解更深刻，将数形结合这一思想方法展现得更加清晰透彻。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
