教材八年级下册第二章第五节介绍了一元一次不等式与一次函数,本节课主要是通过对一元一次不等式与一次函数关系的分析以及实际问题的解决,体会数形结合的思想方法。
(一)教学片段
教师:画出y=2x-5的图像(如图9-2所示)后,请大家观察图像回答问题。
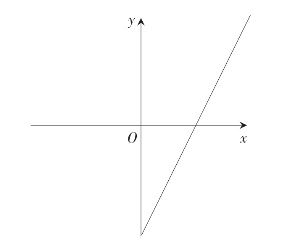
图9-2 图像
教师(问题1):首先,x取何值时,2x-5=0呢?找同学回答一下。
学生1:x=2.5时。
教师(追问):你是如何算出来的呢?
学生1:通过解这个方程得出的。
教师:嗯,很好,这是一种方法。那有没有同学能通过其他方法得到这个答案呢?
学生2:观察图像得出的。
教师:你是如何观察的?
学生2:2x-5=0也就是y=0时,观察图像得出刚好是与x轴的交点。
教师(问题2):嗯,很好。那么x取哪些值时,2x-5﹥0呢?你是如何观察图像看出的?
学生3:x﹥2.5时。因为y=2x-5,2x-5﹥0也就是y﹥0时,观察图像可知在x轴的上方,这时候x﹥2.5。
教师(问题3):嗯,他说得很好。那么x取哪些值时,2x-5﹤0呢?
学生4:x﹤2.5时。因为2x-5﹤0也就是y﹤0时,观察图像可知在x轴的下方,这时候x﹤2.5。
教师(问题4):嗯,那大家想一想,x取哪些值时,2x-5﹥1呢?大家先思考一下,再找同学回答。
学生5:x﹥3时。
教师:你是怎么思考的呢?
学生5:用解一元一次不等式的方法。(https://www.xing528.com)
教师:嗯,这是一个好方法。那有没有同学有不同的想法呢?
(学生认真思考,无人回答)
教师:大家观察一下图像。(教师用PPT展示过y=1作x轴的平行线,与一次函数交于一点,并过此点作y轴的平行线的动态演示过程)当画出了这两条虚线之后,你发现你可以如何观察图像?
学生6:看两条虚线的交点,是(3,1),这个时候x=3,当2x-5﹥1,也就是y﹥1时,是在右边,所以说x﹥3时,2x-5﹥10。
教师:非常好。
(继续讲解下一个例题)
(二)案例评析
本片段选自实习期间刘教师的课堂教学实录,是在引导学生画出一次函数图像后,对一元一次不等式与一次函数相关内容的讲解。接下来,将就问题串在数形结合思想方法教学中的作用和存在的问题这两方面进行评析,并提出改进的建议。
1.作用
本片段通过四个问题串,有意识地引导学生通过观察图像来求解一元一次不等式。这四个问题以层层递进的形式出现,关注学生的“最近发展区”,分别探讨2x-5=0,2x-5﹥0,2x-5﹤0,2x-5﹥1的情况,意在帮助学生理解观察图像的方法,让学生体会解一元一次不等式可以从“数”和“形”两个角度进行分析,充分提升了学生的数学思维。在授课过程中,刘教师充分体现以学生为主体的理念,给予学生充分的思考时间,引导学生解决问题。面对2x-5﹥1的情况,学生观察图像困难,只能从解析式的角度算出答案,但刘教师并没有直接向学生讲授如何通过图像得到答案,而是在让学生观看动态演示过程后继续对学生进行启发诱导,让学生自己总结出答案,让学生在求知的过程中提高学习数学的兴趣。
2.存在的问题
本片段主要是通过让学生体会解一元一次不等式可以从“数”和“形”两个角度分析的形式,帮助学生理解一元一次不等式和一次函数图像的关系,向学生更好地渗透数形结合的思想方法。但由于在讲本节课之前,学生刚刚学习了运用代数的形式解一元一次不等式,由于惯性思维,会不自觉地使他们习惯性地运用之前学过的方法去解决问题,从而轻视用图像求解一元一次不等式的方法。另外,学生对问题4的理解稍有困难,如果教师能结合学生的学习情况,在讲授教材中四个问题的基础上,再举出两个变式性问题,巩固所学知识,加深学生对图形的理解,就会更有效地完成对数形结合的渗透。
3.改进的建议
为了更好地引导学生从函数图像的角度思考问题,避免学生直接求解不等式,教师可对教材中的问题做适当的改编。例如,可设置如下精细化的问题串。
(1)x取何值时,y=0?
(2)x取哪些值时,y﹥0?
(3)x取哪些值时,y﹤0?
(4)x取哪些值时,y﹥1?
(5)x取哪些值时,y﹤-3?
通过这样将教材中的问题作精细化的处理,能够更好地帮助学生从函数图像的角度思考问题,从而更好地渗透数形结合思想。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




