数学的思想影响着整个运算的过程,是学生分析的工具,也是处理数学问题的观点。通过学习数学思想,学生能够掌握整个解题的思路,有助于顺利进行数学计算,透彻理解数学知识。如果不能全面地掌握数学思想(如分类讨论、数形结合、函数与方程等),就会严重影响解题的全面性,从而丢失一部分分数。
(一)分类讨论思想
在解答某些数学问题时,有时候会遇到多种情况,对这些情况加以分类,并逐类求解,然后综合归纳,这就是分类归纳法。分类讨论是一种逻辑方法,也是一种数学思想。有关分类讨论的数学问题具有明显的逻辑性、综合性、探索性,能够训练学生思维的条理性和概括性。因此,在高中试题中占有重要的位置。下面就以两道题讲述分类思想在高中数学中的应用。
例1:若函数f(x)=a+bcosx+csinx的图像经过点(0,1)和(![]() ,1)两点,且x∈[0,
,1)两点,且x∈[0,![]() ]时,|f(x)|≤2恒成立,则实数a的取值范围是_______。
]时,|f(x)|≤2恒成立,则实数a的取值范围是_______。
解析:![]()
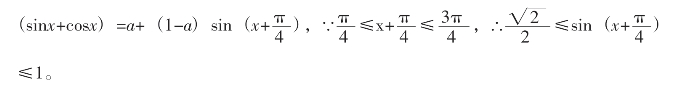
①当a≤1时,1≤f(x)≤a+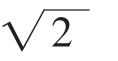 (1-a),∵|f(x)|≤2,∴只要a+
(1-a),∵|f(x)|≤2,∴只要a+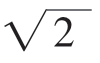 (1-a)≤2,解得a≥-
(1-a)≤2,解得a≥-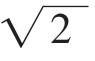 ,∴-2≤a≤1。
,∴-2≤a≤1。
②当a﹥1时,a+(1-a)≤f(x)≤1,∴只要a+(1-a)≥-2,解得a≤4+3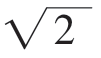 ,∴1﹤a≤4+3
,∴1﹤a≤4+3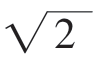 。
。
综合①②可知,实数a的取值范围为[-2,4+3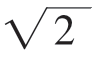 ]。
]。
例2:已知函数f(x)=x|x2-a|,a∈R。
(1)当a≤0时,求证函数f(x)在(-∞,+∞)上是增函数。
(2)当a=3时,求函数f(x)在区间[0,b](b﹥0)上的最大值。
解析:
(1)∵a≤0,∴x2-a≥0,∴f(x)=x(x2-a)=x3-ax,f′(x)=3x2-a,∵f′(x)≥0对x∈R成立,∴函数f(x)在(-∞,+∞)上是增函数。
(2)当a=3时,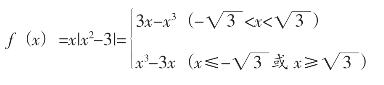
(i)当x﹤-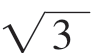 或x﹥
或x﹥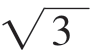 时,f′(x)=3x2-3=3(x-1)(x+1)﹥0。
时,f′(x)=3x2-3=3(x-1)(x+1)﹥0。
(ii)当- ﹤x﹤
﹤x﹤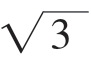 时,f′(x)=3-3x2=-3(x-1)(x+1)。
时,f′(x)=3-3x2=-3(x-1)(x+1)。
当-1﹤x﹤1时,f(x)﹥0;
当-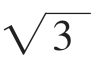 ﹤x﹤-1或1﹤x﹤
﹤x﹤-1或1﹤x﹤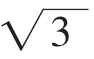 时,f(x)﹤0。
时,f(x)﹤0。
所以f(x)的单调递增区间是(-∞,-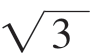 ],[-1,1],[
],[-1,1],[ ,+∞),f(x)的单调递减区间是[-
,+∞),f(x)的单调递减区间是[-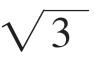 ,-1],[1,
,-1],[1,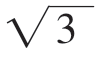 ]。
]。
由区间的定义可知,b﹥0。
①若0﹤b≤1时,则[0,b]∈[-1,1],因此函数f(x)在[0,b]上是增函数,∴当x=b时,f(x)有最大值f(b)=3b-b3。
②若1﹤b≤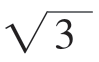 时,f(x)=3x-x3在[0,1]上单调递增,在[1,b]上单调递减,因此在x=1时取到极大值f(1)=2,并且该极大值就是函数f(x)在区间[0,b]上的最大值,所以当x=1时,f(x)有最大值2。
时,f(x)=3x-x3在[0,1]上单调递增,在[1,b]上单调递减,因此在x=1时取到极大值f(1)=2,并且该极大值就是函数f(x)在区间[0,b]上的最大值,所以当x=1时,f(x)有最大值2。
③若b﹥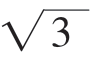 时,当x∈[0,
时,当x∈[0,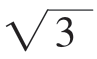 ]时,f(x)=3x-x3在[0,1]上单调递增,在[1,
]时,f(x)=3x-x3在[0,1]上单调递增,在[1,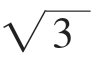 ]上单调递减,因此在x=1时取到极大值f(1)=2;在x∈[
]上单调递减,因此在x=1时取到极大值f(1)=2;在x∈[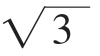 ,b]时,f(x)=x3-3x在[
,b]时,f(x)=x3-3x在[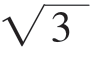 ,b]上单调递增,在x=b时,f(x)有最大值f(b)=b3-3b。
,b]上单调递增,在x=b时,f(x)有最大值f(b)=b3-3b。
当f(1)≥f(b),即2≥b3-3b,b3-b-2b-2≤0,b(b2-1)-2(b+1)≤0,(b+1)2(b-2)≤0,b≤2,∴当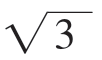 ﹤b≤2时,在x=1时,f(x)取到最大值f(1)=2。
﹤b≤2时,在x=1时,f(x)取到最大值f(1)=2。
当f(1)﹤f(b),解得b﹥2,∴当b﹥2时,f(x)在x=b时,取到最大值f(b)=b3-3b。
综上所述,函数y=f(x)在区间[0,b]上的最大值为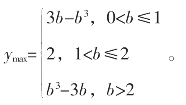
(二)数形结合思想
在古代兵法《三十六计》开篇中有一句话是“数中有术,术中有数”,可以理解为:不同的战争形势自有其对战策略,同时每项对战策略之中,又存在着多种战争的变化形式。同样,在数学中存在着数和形两种最基本的元素。正是基于数和形的抽象研究,才产生了数学这门学科。因此,在研究数学问题时,笔者常常引导学生根据数学问题的条件和结论之间的内在联系,将数的问题利用形来观察,提醒其几何意义,而形的问题也借助于数去思考,分析其代数含义,这样数与形的巧妙结合,会使解题更加快捷灵活,就是我们常说的数形结合的思想。
在高中数学的考试中,选择题和填空题往往使用数形结合方法,即“以形助数”,将数量关系的研究转化为图形性质的研究,使代数问题几何化;在解答题中突出形到数的转化,即“以数解形”,把图形性质的研究转化为数量关系的研究,使几何问题代数化。解析几何就是非常典型的例子,由“形”转到“数”,往往较为明显,也需要学生具备较强的数形结合的意识。
例1:(2014·大纲全国)直线l1和l2是圆x2+y2=2的两条切线,若l1与l2的交点为(1,3),则l1与l2的夹角的正切值等于________。
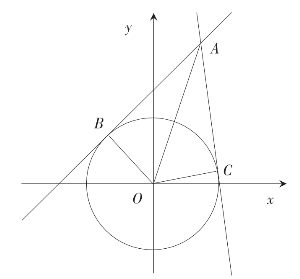
图6-1 例1
利用两点间距离公式及直角三角形求∆AOB各边,进而利用二倍角公式求夹角的正切值。
如图6-1所示,![]()
![]() (https://www.xing528.com)
(https://www.xing528.com)
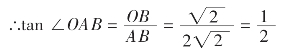 ,∴所求角的正切值为tan∠CAB=
,∴所求角的正切值为tan∠CAB=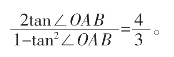
例2:如果实数x,y满足等式x2+y2-4x+1=0,那么![]() 的最大值为_____。解析:初看此题,形式上是一道代数题,但站在代数的角度看,令人茫然无措。把关系式x2+y2-4x+1=0化为(x-2)2+y2=(
的最大值为_____。解析:初看此题,形式上是一道代数题,但站在代数的角度看,令人茫然无措。把关系式x2+y2-4x+1=0化为(x-2)2+y2=(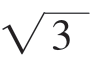 )2,很自然地与圆的方程联系起来。而
)2,很自然地与圆的方程联系起来。而![]() 恰为点(x,y)与原点连线的斜率,这便把问题与“形”结合起来。问题相当于如图6-2所示的几何问题:动点P(x,y)在圆C上运动,求直线OP的斜率的最大值。
恰为点(x,y)与原点连线的斜率,这便把问题与“形”结合起来。问题相当于如图6-2所示的几何问题:动点P(x,y)在圆C上运动,求直线OP的斜率的最大值。
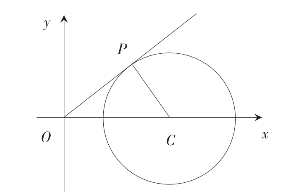
图6-2 例2
观察图6-2易得:当P在第一象限,并且OP与圆C相切时,OP的斜率最大。这时,因为PC⊥OP,所以![]()
(三)函数与方程思想
函数是高中数学的主线,它用联系和运动、变化的观点研究、描述客观世界中相互关联的量之间的依存关系,形成变量数学的一大重要基础和分枝。函数思想以函数知识作基石,用运动变化的观点分析和研究数学对象间的数量关系,使函数知识的应用得到极大的扩展,丰富并优化了数学解题活动,给数学解题带来一股很强的创新能力。因此,越来越成为数学高考的长考不衰的热点。
(2014·新课标全国Ⅱ)设函数f(x)=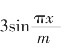 ,若存在f(x)的极值点x0满足
,若存在f(x)的极值点x0满足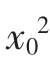 +[f(x0)]2﹤m2,则实数m的取值范围是( )。
+[f(x0)]2﹤m2,则实数m的取值范围是( )。
A.(-∞,-6)∪(6,+∞)
B.(-∞,-4)∪(4,+∞)
C.(-∞,-2)∪(2,+∞)
D.(-∞,-1)∪(1,+∞)
解析:运用正难则反思想,将特称命题与全称命题相互转化,即转化为不等式恒成立问题。
∵f(x)=![]() 的极值点即为函数图像中的最高点或最低点的横坐标,由三角函数的性质可知
的极值点即为函数图像中的最高点或最低点的横坐标,由三角函数的性质可知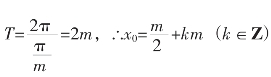 。假设不存在这样的x0,即对任意的x0都有
。假设不存在这样的x0,即对任意的x0都有![]() ,则
,则![]() ,整理得m2(k2+k-
,整理得m2(k2+k-![]() )-3≥0,即
)-3≥0,即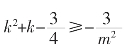 恒成立。因为
恒成立。因为![]() 的最小值为
的最小值为![]() (当k=-1或0时取得),故-2≤m≤2,因此原特称命题成立的条件是m﹥2或m﹤-2。
(当k=-1或0时取得),故-2≤m≤2,因此原特称命题成立的条件是m﹥2或m﹤-2。
例题:(2014·北京)已知函数f(x)=xcosx-sinx,x∈[0,![]() ]。
]。
(1)求证:f(x)≤0。
(2)若![]() 恒成立,则求a的最大值与b的最小值。
恒成立,则求a的最大值与b的最小值。
解析:
(1)证明:由f(x)=xcosx-sinx,得f′(x)=cosx-xsinx-cosx=-xsinx。因为在区间(0,![]() )上f′(x)=-xsinx﹤0,所以f(x)在区间(0,
)上f′(x)=-xsinx﹤0,所以f(x)在区间(0,![]() )上单调递减,从而f(x)≤f(0)=0。
)上单调递减,从而f(x)≤f(0)=0。
(2)当x﹥0时,![]() 等价于“sinx-ax﹥0”,
等价于“sinx-ax﹥0”,![]() 等价于“sinx-bx﹤0”。
等价于“sinx-bx﹤0”。
令g(x)=sinx-cx,则g′(x)=cosx-c。
当c≤0时,g(x)﹥0对任意x∈(0,![]() )恒成立。
)恒成立。
当c≥1时,因为对任意x∈(0,![]() ),g′(x)=cosx-c﹤0,所以g(x)在区间[0,
),g′(x)=cosx-c﹤0,所以g(x)在区间[0,![]() ]上单调递减,从而g(x)﹤g(0)=0对任意x∈(0,
]上单调递减,从而g(x)﹤g(0)=0对任意x∈(0,![]() )恒成立。
)恒成立。
当0﹤c﹤1时,存在唯一的x0∈(0,![]() )使得g′(x0)=cosx0-c=0。
)使得g′(x0)=cosx0-c=0。
g(x)与g′(x)在区间(0,![]() )上的情况如表6-1所示:
)上的情况如表6-1所示:
表6-1 g(x)与g′(x)在区间(0,![]() )上的情况
)上的情况

因为g(x)在区间[0,x0]上是增函数,所以g(x0)﹥g(0)=0。进一步,“g(x)﹥0对任意x∈(0,![]() )恒成立”当且仅当
)恒成立”当且仅当![]() ,即0﹤
,即0﹤![]()
综上所述,当且仅当c≤![]() 时,g(x)﹥0对任意x∈(0,
时,g(x)﹥0对任意x∈(0,![]() )恒成立;当且仅当c≥1时,g(x)﹤0对任意x∈(0,
)恒成立;当且仅当c≥1时,g(x)﹤0对任意x∈(0,![]() )恒成立。所以,若
)恒成立。所以,若![]() 对任意x∈(0,
对任意x∈(0,![]() )恒成立,则a的最大值为
)恒成立,则a的最大值为![]() ,b的最小值为1。
,b的最小值为1。
(四)转化与化归思想
所谓转化与化归思想,就是在研究和解决有关数学问题时,采用某种手段,将问题通过变换使之转化归结为在已有知识范围内可以解决的一种方法。数学中的一切问题的解决都离不开转化与化归。数形结合思想体现了数与形的转化,函数与方程思想体现了函数、方程与不等式之间的相互转化,分类讨论思想体现了局部与整体之间的相互转化。以上三种思想方法都是转化与化归思想的具体体现,各种变换方法、分析法、反证法、待定系数法、构造法等都是转化与化归思想的体现。所以说,转化与化归思想是数学思想方法的灵魂。
(2014·新课标全国Ⅰ)设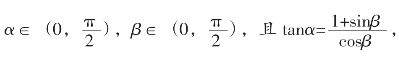 则( )。
则( )。

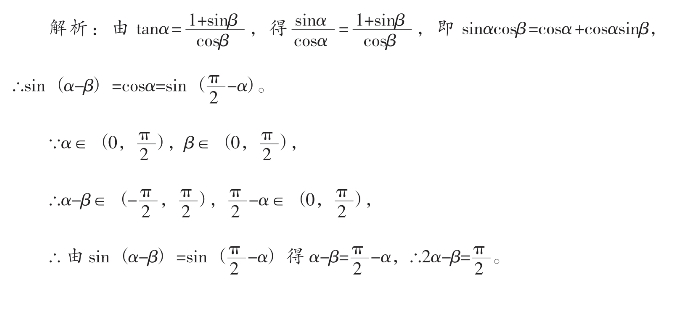
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




