高中数学教学：核心素养应用案例一

（一）数学概念教学设计

数学概念是人脑对现实对象的数量关系和空间形式的本质特征的一种反映形式，即一种数学的思维形式。在数学概念的教学中，分为以下四步：概念的引入→概念的形成→概念的强化→概念的应用。

学生通过对概念的学习来提升直观想象能力有重要的意义。教材的知识点中并非只有向量等几何部分能够培养学生的直观想象能力，在集合、数列等部分也可以提升直观想象能力。下面，笔者就以数列的概念作为案例进行讲解。

环节1：概念的导入。

教师举例：数学中的数列，还有三角形、四边形、五边形、六边形，如图5-1所示。

图5-1　三角形　四边形　五边形　六边形

现实生活中也有很多的数列，如图5-2所示的倒置三角中的圆。

图5-2　倒置三角图

师生活动：通过多媒体依次展示实例中的图片，引导学生发现其中的规律。

设计意图：通过具体案例，学生能够初步了解到数列的概念，激发学习的兴趣。在生活化的情境中，学生可以体会其中的变化规律，初步得到这种规律，从而得出数列的概念。

环节2：概念的形成。

思考：结合上述的数列形成过程进行观察，大家能否发现其中有何共同之处？

师生活动：每个数列都按照一定的顺序排布，前后数的差值符合一定的规律。教师引导学生归纳概念，在引出定义的基础上，给出数列各项的形式a1，a2，a3，……an……学生进行猜想，将数列分为有穷数列、无穷数列、等差数列、等比数列等。

设计意图：联系前面的实例，进行猜想、归纳，得出数列概念的内在本质，再进行概括得到概念。

环节3：概念的强化。

提问1：“4，5，6，7，8”和“4，6，5，8，7”是否为同一个数列？

学生：不是，数列中的元素具有一定的顺序和确定性。

提问2：大家可以对数列和函数进行类比，我们发现数列的概念非常强调有序性，即数列的每一项n都有唯一对应的选项an与之对应。

具体如表5-1所示。

表5-1　序号n与项an的对应关系

笔者运用几何画板软件，为学生动态展示表5-1中的点，如图5-3所示。

图5-3　表格对应图

提问3：结合表格和图形，能否想到以前学过的知识？

设计意图：通过知识的迁移，引导学生想起函数的概念，通过列表法和图形的结合，以函数的解析式来得到数列的通项公式，使他们能够容易接受。

（二）数学结论的教学设计(www.xing528.com)

数学结论是指已经证明正确的命题，如公式、定理等。在数学概念的教学中，分为以下四步：结论的引入→结论的分析→结论的证明→结论的应用。

数学结论的证明是数学教学的主要内容，具有抽象度高、难度大的特点。在数学授课中，教师如果能够借助于直观表达，为学生展示数学结论的几何意义及证明就会加深他们的理解程度。笔者选取基本不等式的证明作为案例来提升学生的直观想象能力。

教学分析：

本节课位于不等式的基础内容之后，学生需要学会推导并掌握基本不等式，理解这个基本不等式的几何意义，并掌握定理中的不等号“≥”取等号的条件是：当且仅当这两个数相等。从核心素养的角度看，借助于直观的图形，学生能够在具体的学习情境中通过对图形的观察，分析图形与数量间的关系，解决教师提出的问题，形成“数形结合”的思想，养成初步运用图形解决问题的能力。

环节1：创设问题情境，引入不等式概念。

问题情境1：如图5-4是在北京召开的第24届国际数学家大会的会标，会标是根据中国古代数学家赵爽的弦图设计的，它看上去像一个风车，代表中国人民热情好客。你能在这个图案中找出一些相等关系或不等关系吗？

图5-4　赵爽弦图

师生活动：根据赵爽弦图，笔者引导学生从面积的关系来找到不等关系，即a2+b2﹥2ab，通过动画直观感受到，当a=b时，得到等式a2+b2=2ab。在此基础上，学生要应用来代替a，b，进而得出在a﹥0，b﹥0的情况下基本不等式。

设计意图：通过赵爽弦图，学生运用数形结合的思想来分析、抽象得到基本不等式，借助于几何画板的动态演示形成直观感受，从而提升直观想象能力。

环节2：初步认识基本不等式，理解表达的意义。

师生活动：

提问1：大家观察下，能否说出与a，b分别存在着怎样的代数和几何关系？

学生：在a﹥0，b﹥0的情况下是二者的“平均数”，则是矩形（a，b为边长）面积的开方。

教师：通过大家上述的论述，从数学运算的角度，定义为正数a和b的“平均数”，称为“算数平均数”；从几何的角度，定义是长为a、宽为b的矩形面积相等的正方形的边长，称为“几何平均数”。

提问2：大家想下，如何对基本不等式用文字语言进行描述呢？

学生：两个正数的算术平均数不小于它们的几何平均数。

设计意图：学生通过基本不等式深挖背后隐藏的本质内容，用严谨的语言描述基本不等式的结构，从而深化对基本不等式概念的理解，提升图形和语言能力。

环节3：基本不等式的证明。

探究一：图5-5是笔者运用几何画板画出的图形。其中，假设AC为圆的直径，AB=a，BC=b，过点B、O作AC的垂线EB、DO，其中E、D是圆上的点，试分析图中线段的长度，根据这个图形是否能得到基本不等式的几何解释？

图5-5　基本不等式证明图

学生：根据图形纷纷展开思考，通过∆ABE∽∆EBC，得，所以DO≥EB，即

探究二：在学生进行完探究一的基础上，笔者要求学生进行本次探究，设BC是圆O的直径，延长线段CB到点A，AB=a，AC=b，AD与圆相切于点D，试分析图5-6中线段的长度，根据这个图形是否能得到基本不等式的几何解释？

学生：在Rt∆ADO中，，由直角边小于斜边，得到

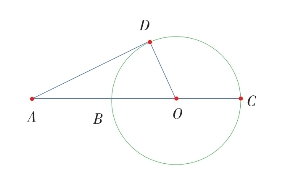
图5-6　基本不等式证明

设计意图：通过几何图形，学生能够在熟悉的情境中探究基本不等式的几何解释。在不等式教学中，笔者通过几何图形来讲授基本不等式的证明过程，这有利于提升学生的直观想象能力，引导他们更深层次地理解相关概念，在潜移默化中培养其几何思维。