高中数学教学的核心函数概念

（一）一次函数

现实背景：做匀速直线运动的物体，运动的速度（位移与时间的比值）是定值。在运动的过程中，瞬时速度与平均速度相等。

决定运动状态的要素：速度v、时间t和位移S，这里v值是常量，而t和S则是变量。

各要素之间存在的关系：随着时间的变化，位移发生变化，即是一个常量，时间与位移是一一对应的关系。

数学模型：对于不同的问题，有各种各样的一次函数，在此基础上，我们进行归纳，即得到y=kx+b。这里需要注意的是，b是初始条件，y的值随着x的变化而变化。

虽然一次函数较为简单，但是应用范围较广，在物理、化学中有着广泛的应用。

（二）二次函数

现实背景：物体做匀加速直线运动，在运动过程中，物体速度的变化与时间的比值是定值，即速度的变化不变。

决定运动状态的要素：加速度a、初速度v0、时间t和位移S。其中，a和v0是常量，t和S是变量，速度随着时间的变化而均匀改变。(www.xing528.com)

各要素之间的关系：是一个定值，给定一个时间，位移与之相对应。如果在初始条件中，t=0，v=v0，S=S0，则运动的规律就是

数学模型：在不同类型的问题中，有不同的二次函数，如自由落体的运动规律为，动能定理的表达式为等。通过对二次函数进行归纳，我们得到的表达式为y=ax2+bx+c。

（三）反比例函数

现实背景：在同一个电路中，导体中的电流与它两点的电压和电阻有关系。这种运动的特征是，两个变量的乘积为常量。

决定变化状态的要素：电流I、电压U、电阻R。

各要素之间的关系：根据已经学习过的欧姆定律，得到以下公式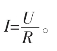

数学模型：在物理、化学中存在着大量的规律，通过归纳分析，我们可以得到反比例函数的表达式为，其中k为常数。